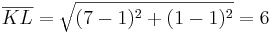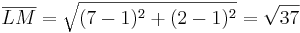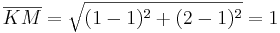Schluss: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Lösung eingefügt)
(Lösung eingefügt)
Zeile 31: Zeile 31:
 
*<math>\Leftrightarrow (\sqrt{37})^2=6^2+1^2</math>
 
*<math>\Leftrightarrow (\sqrt{37})^2=6^2+1^2</math>
 
*<math>\Leftrightarrow {37=37\,}</math><br /><br />
 
*<math>\Leftrightarrow {37=37\,}</math><br /><br />
−
*Der Satz des Pythagoras ergibt eine wahre Aussage, also muss das Dreieck rechtwinklig sein
+
*Der Satz des Pythagoras ergibt eine wahre Aussage, also muss das Dreieck <math>\triangle{KLM}</math> rechtwinklig sein
 +
}}
 +
 
 +
 
 +
b) {{Lösung versteckt|
 +
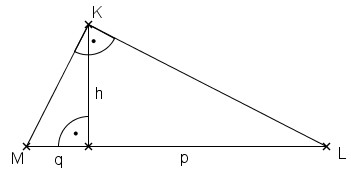
*Im Folgenden siehst du eine '''Skizze''' zur Aufgabenstellung:<br />
 +
[[Bild:Lernpfad_SdP_Skizze_SdP_1b.png]]<br />
 +
*h soll berechnet werden, das geht über zwei Ansätze:
 +
*'''1)''' Höhe über den Satz des Pythagoras in einem der kleineren rechtwinkligen Dreiecke berechnen
 +
*'''2)''' Höhe über den Höhensatz berechnen<br /><br />
 +
 
 +
'''1.Möglichkeit:'''
 +
*Man berechnet zunächst p oder q über den Kathetensatz:<br />
 +
*<math>(\overline{MK})^2=\overline{ML} \cdot q</math>
 +
*<math>q=\frac{(\overline{MK})^2}{\overline{ML}}=\frac{36}{\sqrt{37}} \approx 5,92</math><br /><br />
 +
 
 +
*Danach setzt man den Satz des Pythagoras für das entsprechende rechtwinklige Dreieck an:<br />
 +
*<math>(\overline{MK})^2=h^2+q^2</math>
 +
*<math>h^2=(\overline{MK})^2-q^2</math>
 +
*<math>h=\sqrt{(\overline{MK})^2-q^2}=\sqrt{6^2-(5,92)^2} \approx 0,99</math><br /><br />
 +
 
 +
'''2.Möglichkeit:'''
 +
*Man berechnet zunächst p oder q über den Kathetensatz:<br />
 +
*<math>(\overline{KL})^2=\overline{ML} \cdot p</math>
 +
*<math>p=\frac{(\overline{KL})^2}{\overline{ML}}=\frac{1}{\sqrt{37}} \approx 0,16</math><br /><br />
 +
 
 +
*Danach berechnet man den fehlenden Hypotenusenabschnitt:<br />
 +
*<math>{h=p+q\,}</math>
 +
*<math>q=h-p=\sqrt{37}-0,16 \approx 5,92</math><br /><br />
 +
 
 +
*Jetzt kann man die Höhe über den Höhensatz berechnen:<br />
 +
*<math>h^2=p \cdot q</math>
 +
*<math>h=\sqrt{p \cdot q}=\sqrt{(0,16) \cdot (5,92)} \approx 0,99</math>
 
}}
 
}}
 
==Aufgabe 2==
 
==Aufgabe 2==

Version vom 25. Januar 2009, 13:44 Uhr

Arbeitsauftrag:

  • Hole dir das Arbeitsblatt Die Satzgruppe des Pythagoras
  • Fülle das Arbeitsblatt anhand der im Lernpfad gelernten Sätze aus
  • HINWEIS: Solltest du dir bei einem der Sätze nicht mehr sicher sein, lies noch einmal im Heft oder im Lernpfad nach
  • Vergleiche deine Lösungen mit den Einträgen aus dem Heft oder mit den entsprechenden Seiten des Lernpfades


Arbeitsauftrag:

  • Hole dir das Übungsblatt zur Satzgruppe des Pythagoras
  • Löse die Aufgaben und vergleiche sie mit den unten stehenden Lösungen


Aufgabe 1

a)

  • Wenn das Dreieck 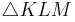\triangle{KLM} rechtwinklig ist, ergibt der Satz des Pythagoras eine wahre Aussage
  • Man muss also den Satz des Pythagoras für das Dreieck ansetzen
  • Dazu berechnet man zunächst die einzelnen Seitenlängen:
  • \overline{KL}=\sqrt{(7-1)^2+(1-1)^2}=6
  • \overline{LM}=\sqrt{(7-1)^2+(2-1)^2}=\sqrt{37}
  • \overline{KM}=\sqrt{(1-1)^2+(2-1)^2}=1


  • Nun kann man den Satz des Pythagoras ansetzen
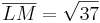  • \overline{LM}=\sqrt{37} ist die längste Seite des Dreiecks und wäre auch die Hypotenuse

  • Daraus folgt der Ansatz:

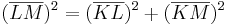
  • (\overline{LM})^2=(\overline{KL})^2+(\overline{KM})^2
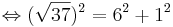
  • \Leftrightarrow (\sqrt{37})^2=6^2+1^2
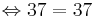
  • \Leftrightarrow {37=37\,}

  • Der Satz des Pythagoras ergibt eine wahre Aussage, also muss das Dreieck 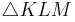\triangle{KLM} rechtwinklig sein


b)

  • Im Folgenden siehst du eine Skizze zur Aufgabenstellung:

Lernpfad SdP Skizze SdP 1b.png

  • h soll berechnet werden, das geht über zwei Ansätze:
  • 1) Höhe über den Satz des Pythagoras in einem der kleineren rechtwinkligen Dreiecke berechnen
  • 2) Höhe über den Höhensatz berechnen

1.Möglichkeit:

  • Man berechnet zunächst p oder q über den Kathetensatz:
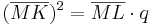
  • (\overline{MK})^2=\overline{ML} \cdot q
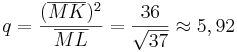
  • q=\frac{(\overline{MK})^2}{\overline{ML}}=\frac{36}{\sqrt{37}} \approx 5,92

  • Danach setzt man den Satz des Pythagoras für das entsprechende rechtwinklige Dreieck an:
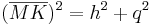
  • (\overline{MK})^2=h^2+q^2
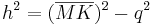
  • h^2=(\overline{MK})^2-q^2
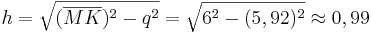
  • h=\sqrt{(\overline{MK})^2-q^2}=\sqrt{6^2-(5,92)^2} \approx 0,99

2.Möglichkeit:

  • Man berechnet zunächst p oder q über den Kathetensatz:
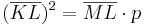
  • (\overline{KL})^2=\overline{ML} \cdot p
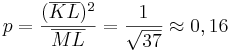
  • p=\frac{(\overline{KL})^2}{\overline{ML}}=\frac{1}{\sqrt{37}} \approx 0,16

  • Danach berechnet man den fehlenden Hypotenusenabschnitt:
  • {h=p+q\,}
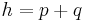
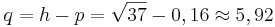
  • q=h-p=\sqrt{37}-0,16 \approx 5,92

  • Jetzt kann man die Höhe über den Höhensatz berechnen:
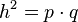
  • h^2=p \cdot q
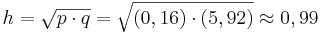
  • h=\sqrt{p \cdot q}=\sqrt{(0,16) \cdot (5,92)} \approx 0,99

Aufgabe 2

Aufgabe 3

Aufgabe 4

Aufgabe 5

Symbol thumbs up.svg Sehr schön! Du hast den Lernpfad zur Satzgruppe des Pythagoras jetzt beendet Symbol thumbs up.svg
Von „http://rmg.zum.de/index.php?title=Lernpfad_zur_Satzgruppe_des_Pythagoras/Schluss&oldid=12417“