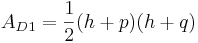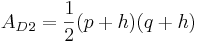Höhensatz: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Beweis zum Höhensatz eingefügt und Lösung verändert)
K (Arbeitsauftrag geänder und Rechtschreibung in Lösung verbessert)
Zeile 62: Zeile 62:
 
*''Was fällt dir auf?''
 
*''Was fällt dir auf?''
  
−
*''Was kann man daraus folgern?''</div>
+
*''Was kann man daraus für den Flächeninhalt der blauen Teile folgern?''</div>
  
  
Zeile 78: Zeile 78:
 
{{Lösung versteckt|
 
{{Lösung versteckt|
 
'''Folgerung:'''
 
'''Folgerung:'''
−
*Die Dreiecke sind Flächengleich
+
*Die Dreiecke sind flächengleich
 
*In beiden Dreiecken tauchen das rote und das gelbe Dreieck auf
 
*In beiden Dreiecken tauchen das rote und das gelbe Dreieck auf
 
*Der blaue Flächeninhalt in beiden Dreiecken muss also die gleiche Fläche haben, da:
 
*Der blaue Flächeninhalt in beiden Dreiecken muss also die gleiche Fläche haben, da:

Version vom 6. Dezember 2008, 16:56 Uhr

Der Höhensatz

Ein weiterer Satz aus der Satzgruppe des Pythagoras ist der Höhensatz.

Benennung rechtwinkliges Dreieck für Höhensatz.png

Bevor du dich jedoch näher mit diesem Satz beschäftigst, musst du erst noch einige neue Bezeichnungen für Seiten in rechtwinkligen Dreiecken lernen:

  • Die Höhe in einem rechtwinkligen Dreieck steht immer senkrecht auf die Hypotenuse

  • Die Höhe teilt die Hypotenuse in zwei Teile, die Hypotenusenabschnitte
    (in der Zeichnung p und q)

  • Die Hypotenuseabschnitte liegen jeweils an einer der beiden Katheten an
  • In diesem Fall kann man sagen:
  • p liegt an der Kathete a an
  • q liegt an der Kathete b an


Arbeitsauftrag:

  • Zeichne das rechtwinklige Dreieck mit den Bezeichnungen in dein Heft
  • Notiere dir die Bemerkungen rechts vom rechtwinkligen Dreieck
  • Was kann man daraus folgern?


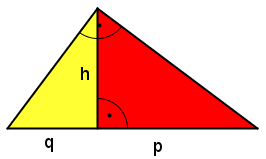
  • Ausgangspunkt für die folgende Überlegung ist ein rechtwinkliges Dreieck mit der Höhe h und den Hypotenusenabschnitten p und q

Beweis zu Höhensatz 1.png

  • Aus diesem rechtwinkligen Dreieck kann man zwei kleinere rechtwinklige Dreiecke machen
  • Eines hat als Länge der Katheten p und h, das andere hat Katheten der Längen q und h

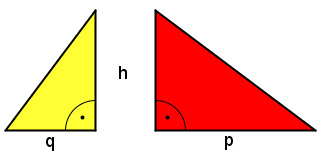
Beweis zu Höhensatz 2.png


  • Diese beiden rechtwinkligen Dreiecke kann man nun verschieden aneinander anlegen und so ein neues Dreieck erzeugen
  • Die zwei Möglichkeiten seht ihr in den beiden folgenden Grafiken

Beweis zu Höhensatz 3a.png

Beweis zu Höhensatz 3b.png

Arbeitsauftrag:

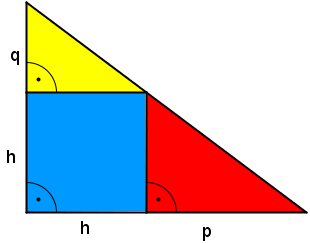
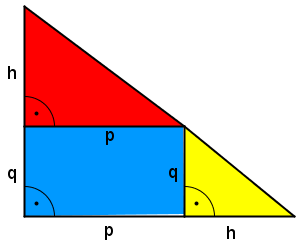
  • Hole dir das Arbeitsblatt Beweis zum Höhensatz
  • Berechne auf dem Arbeitsblatt den Flächeninhalt der beiden unten stehenden Dreiecke!
  • Was fällt dir auf?
  • Was kann man daraus für den Flächeninhalt der blauen Teile folgern?


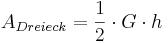
Der Flächeninhalt eines Dreiecks berechnet sich so: A_{Dreieck}=\frac{1}{2} \cdot G \cdot h

Fläche für Dreieck 1:

  • {A_D}_1=\frac{1}{2}(h+p)(h+q)

Fläche für Dreieck 2:

  • {A_D}_2=\frac{1}{2}(p+h)(q+h)

Folgerung:

  • Die Dreiecke sind flächengleich
  • In beiden Dreiecken tauchen das rote und das gelbe Dreieck auf
  • Der blaue Flächeninhalt in beiden Dreiecken muss also die gleiche Fläche haben, da:
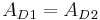
  • {A_D}_1={A_D}_2
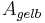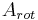  • {A_{gelb}\,} und {A_{rot}\,} in beiden Dreiecken gleich
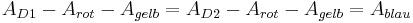
  • Daraus folgt:{A_D}_1-A_{rot}-A_{gelb}={A_D}_2-A_{rot}-A_{gelb}=A_{blau}

  • Das heißt der Flächeninhalt der beiden blauen Dreiecke muss gleich sein

Da 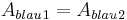{A_{blau}}_1={A_{blau}}_2kann man sagen:

{h^2=pq\,}

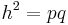
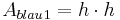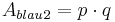
Denn {A_{blau}}_1=h \cdot h und {A_{blau}}_2=p \cdot q

Du hast den Höhensatz bewiesen. Hier geht es nun zum Hefteintrag.

Von „http://rmg.zum.de/index.php?title=Lernpfad_zur_Satzgruppe_des_Pythagoras/Höhensatz&oldid=10604“