Abstandsbestimmung von Punkten: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (internen Link geändert) |
(Rechnung geändert) |
||
| Zeile 46: | Zeile 46: | ||
Hier findest du die '''Lösung zur Berechnung des Abstandes''' von A und B:<br /><br /> | Hier findest du die '''Lösung zur Berechnung des Abstandes''' von A und B:<br /><br /> | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| − | <math>{d^2=(4-1)^2+( | + | <math>{d^2=(4-1)^2+(2,5-0,5)^2\,}</math><br /> |
<math>{d^2=9+4\,}</math><br /> | <math>{d^2=9+4\,}</math><br /> | ||
<math>d=\sqrt{13}</math> | <math>d=\sqrt{13}</math> | ||
Version vom 29. November 2008, 13:45 Uhr
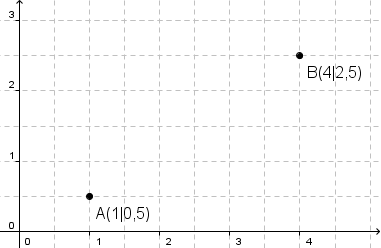
Mit dem Satz des Pythagoras ist es jetzt auch möglich den Abstand von zwei Punkten in einem karthesischen Koordinatensystem zu ermitteln.
Arbeitsauftrag:
- Übertrage die Punkte unter der Überschrift "Abstandsbestimmung von Punkten" in ein Koordinatensystem in deinem Heft
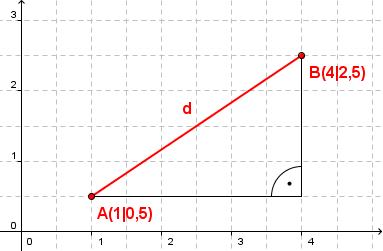
- Sieh dir das Bild an und überlege wie man den Abstand der Punkte berechnen könnte
- Wenn du eine Idee hast vergleiche sie mit den Tips
- Solltest du keine Idee haben, sieh dir die Tips an, vielleicht helfen sie dir
- Berechne den Abstand in deinem Heft und vergleiche deine Rechnung mit der Lösung am Ende der Seite
Sollte dir nichts auffallen, hier ein kleiner Tip
- Man sucht sich ein rechtwinkliges Dreieck in dem man über den Satz des Pythagoras den Abstand berechnen kann
- Jetzt muss man sich nur noch Gedanken über die Länge der Katheten machen
Immer noch nichts? Hier noch ein Tip:
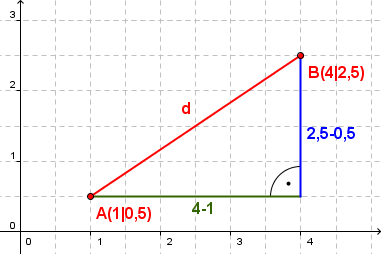
- Die Länge der beiden Katheten berechnet sich über die x- und y-Koordinateneinträge der beiden Punkte
- Für die Länge der x-Kathete zieht man vom x-Eintrag des Punktes B den x-Eintrag des Punktes A ab
- Bei der y-Kathete funktioniert das genauso
Hier findest du die Lösung zur Berechnung des Abstandes von A und B:
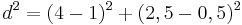
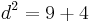
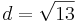
Wenn du die Aufgabe gerechnet hast, geht es hier zum Hefteintrag zum Thema.