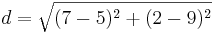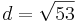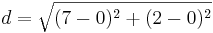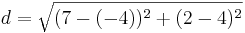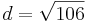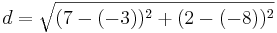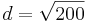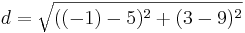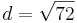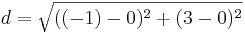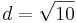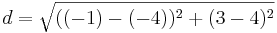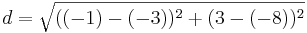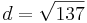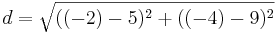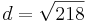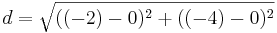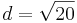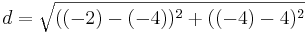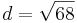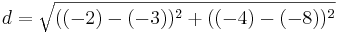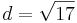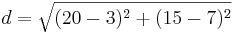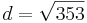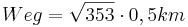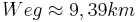Lösungen für das Übungsblatt zur Abstandsbestimmung von Punkten: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
K
K
 
(5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
Hier wird ein Verweis auf ein Übungsblatt stehen und die Lösungen werden noch eingefügt.<br /><br />
+
Hole dir das '''Übungsblatt zur Abstandsbestimmung von Punkten'''.<br /><br />
 +
== Aufgabe 1==
 +
Für '''P(7|2)''' {{Lösung versteckt|
 +
a) A(5,9)
 +
*<math>d=\sqrt{(7-5)^2+(2-9)^2}</math>
 +
*<math>d=\sqrt{53}</math><br />
  
−
Wenn du alle Aufgaben berechnet hast geht es [[Höhensatz 1|hier]] zum nächsten Satz der Satzgruppe des Pythagoras
+
b) U(0,0)
 +
*<math>d=\sqrt{(7-0)^2+(2-0)^2}</math>
 +
*<math>d=\sqrt{53}</math><br />
 +
 
 +
c) C(-4,4)
 +
*<math>d=\sqrt{(7-(-4))^2+(2-4)^2}</math>
 +
*<math>d=\sqrt{106}</math><br />
 +
 
 +
d) D(-3,-8)
 +
*<math>d=\sqrt{(7-(-3))^2+(2-(-8))^2}</math>
 +
*<math>d=\sqrt{200}</math><br />
 +
}}<br /><br />
 +
 
 +
Für '''Q(-1|3)''' {{Lösung versteckt|
 +
a) A(5,9)
 +
*<math>d=\sqrt{((-1)-5)^2+(3-9)^2}</math>
 +
*<math>d=\sqrt{72}</math><br />
 +
 
 +
b) U(0,0)
 +
*<math>d=\sqrt{((-1)-0)^2+(3-0)^2}</math>
 +
*<math>d=\sqrt{10}</math><br />
 +
 
 +
c) C(-4,4)
 +
*<math>d=\sqrt{((-1)-(-4))^2+(3-4)^2}</math>
 +
*<math>d=\sqrt{10}</math><br />
 +
 
 +
d) D(-3,-8)
 +
*<math>d=\sqrt{((-1)-(-3))^2+(3-(-8))^2}</math>
 +
*<math>d=\sqrt{137}</math><br />
 +
}}<br /><br />
 +
 
 +
Für '''S(-2|-4)''' {{Lösung versteckt|
 +
a) A(5,9)
 +
*<math>d=\sqrt{((-2)-5)^2+((-4)-9)^2}</math>
 +
*<math>d=\sqrt{218}</math><br />
 +
 
 +
b) U(0,0)
 +
*<math>d=\sqrt{((-2)-0)^2+((-4)-0)^2}</math>
 +
*<math>d=\sqrt{20}</math><br />
 +
 
 +
c) C(-4,4)
 +
*<math>d=\sqrt{((-2)-(-4))^2+((-4)-4)^2}</math>
 +
*<math>d=\sqrt{68}</math><br />
 +
 
 +
d) D(-3,-8)
 +
*<math>d=\sqrt{((-2)-(-3))^2+((-4)-(-8))^2}</math>
 +
*<math>d=\sqrt{17}</math><br />
 +
}}<br />
 +
 
 +
== Aufgabe 2==
 +
{{Lösung versteckt|
 +
Wir müssen zunächst den Abstand der beiden Punkte Z(20,15) und S(3,7) berechnen:
 +
*<math>d=\sqrt{(20-3)^2+(15-7)^2}</math>
 +
*<math>d=\sqrt{353}</math><br />
 +
 
 +
Tine muss also <math>\sqrt{353}</math> Einheiten im Koordinatensystem zurücklegen. Da eine Einheit 0,5km entspricht kann man sagen:
 +
*<math>Weg=\sqrt{353} \cdot 0,5km</math>
 +
*<math>Weg \approx 9,39km</math><br />
 +
 
 +
Tine müsste also 9,39km zum Schwimmbad laufen.
 +
}}
 +
 
 +
 
 +
Wenn du alle Aufgaben berechnet hast geht es [[Lernpfad zur Satzgruppe des Pythagoras/Höhensatz|hier]] zum nächsten Satz der Satzgruppe des Pythagoras

Aktuelle Version vom 24. Januar 2009, 18:59 Uhr

Hole dir das Übungsblatt zur Abstandsbestimmung von Punkten.

Aufgabe 1

Für P(7|2)

a) A(5,9)

  • d=\sqrt{(7-5)^2+(2-9)^2}
  • d=\sqrt{53}

b) U(0,0)

  • d=\sqrt{(7-0)^2+(2-0)^2}
  • d=\sqrt{53}

c) C(-4,4)

  • d=\sqrt{(7-(-4))^2+(2-4)^2}
  • d=\sqrt{106}

d) D(-3,-8)

  • d=\sqrt{(7-(-3))^2+(2-(-8))^2}
  • d=\sqrt{200}


Für Q(-1|3)

a) A(5,9)

  • d=\sqrt{((-1)-5)^2+(3-9)^2}
  • d=\sqrt{72}

b) U(0,0)

  • d=\sqrt{((-1)-0)^2+(3-0)^2}
  • d=\sqrt{10}

c) C(-4,4)

  • d=\sqrt{((-1)-(-4))^2+(3-4)^2}
  • d=\sqrt{10}

d) D(-3,-8)

  • d=\sqrt{((-1)-(-3))^2+(3-(-8))^2}
  • d=\sqrt{137}


Für S(-2|-4)

a) A(5,9)

  • d=\sqrt{((-2)-5)^2+((-4)-9)^2}
  • d=\sqrt{218}

b) U(0,0)

  • d=\sqrt{((-2)-0)^2+((-4)-0)^2}
  • d=\sqrt{20}

c) C(-4,4)

  • d=\sqrt{((-2)-(-4))^2+((-4)-4)^2}
  • d=\sqrt{68}

d) D(-3,-8)

  • d=\sqrt{((-2)-(-3))^2+((-4)-(-8))^2}
  • d=\sqrt{17}

Aufgabe 2

Wir müssen zunächst den Abstand der beiden Punkte Z(20,15) und S(3,7) berechnen:

  • d=\sqrt{(20-3)^2+(15-7)^2}
  • d=\sqrt{353}

Tine muss also 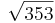\sqrt{353} Einheiten im Koordinatensystem zurücklegen. Da eine Einheit 0,5km entspricht kann man sagen:

  • Weg=\sqrt{353} \cdot 0,5km
  • Weg \approx 9,39km

Tine müsste also 9,39km zum Schwimmbad laufen.


Wenn du alle Aufgaben berechnet hast geht es hier zum nächsten Satz der Satzgruppe des Pythagoras

Von „http://rmg.zum.de/index.php?title=Lernpfad_zur_Satzgruppe_des_Pythagoras/Lösungen_für_das_Übungsblatt_zur_Abstandsbestimmung_von_Punkten&oldid=12325“