Benutzer:Hauck Anne: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: {{ggb/Test.ggb/Datei}}) |
K |
||
| (19 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | =='''''Lösung der Hausaufgabe vom Aufgabenblatt 2 S.216/Nr.10'''''== | ||
| + | |||
| + | ===''Aufgabenstellung:''=== | ||
| + | Wie groß ist die Fläche, die vom Graphen G<sub>f</sub> der Funktion f(x)=<math>\frac{-1}{3}x^2+2x+1</math>, der Ordinate des höchsten Punktes, der x-Achse und der y-Achse eingeschlossen wird? | ||
| + | |||
| + | ===''Lösungsweg:''=== | ||
| + | |||
| + | 1. Bestimme die Nullstellen: | ||
| + | f(x)=0 für ? | ||
| + | <math>\frac{-1}{3}x^2+2x+1=0</math> | ||
| + | <math>\frac{-1}{3}(x^2-6x)=-1</math> | ||
| + | <math>x^2-6x=3</math> | ||
| + | <math>x^2-6x-3=0</math> | ||
| + | <math>x_{1/2}=</math> <math>\frac{-b^+-\sqrt{b^2-4*a*c}}{2*a}</math> | ||
| + | |||
| + | 2. Bestimme das Integral von 0 bis zum x-Wert der Nullstelle, der in positiver x-Richtung liegt: | ||
| + | |||
| + | Veranschaulichung mit Geogebra | ||
{{ggb/Test.ggb/Datei}} | {{ggb/Test.ggb/Datei}} | ||
Aktuelle Version vom 29. September 2008, 17:17 Uhr
Lösung der Hausaufgabe vom Aufgabenblatt 2 S.216/Nr.10
Aufgabenstellung:
Wie groß ist die Fläche, die vom Graphen Gf der Funktion f(x)=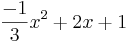
, der Ordinate des höchsten Punktes, der x-Achse und der y-Achse eingeschlossen wird?
Lösungsweg:
1. Bestimme die Nullstellen:
f(x)=0 für ?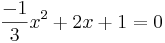
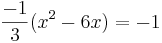
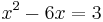
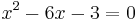
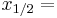
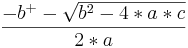
2. Bestimme das Integral von 0 bis zum x-Wert der Nullstelle, der in positiver x-Richtung liegt:
Veranschaulichung mit Geogebra Datei:Veranschaulichung AB2 S.216/Nr.10.jpg
