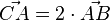Abi 2016 Geometrie I Teil A: Unterschied zwischen den Versionen
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | |||
| − | |||
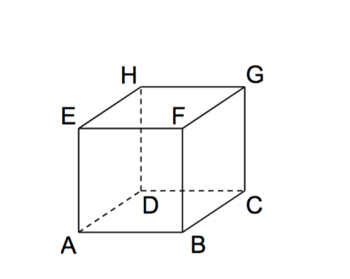
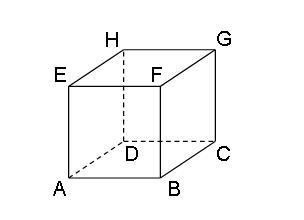
1) Betrachtet wird der abgebildete Würfel ABCDEFGH. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: D(0|0|-2),E(2|0|0), F(2|2|0) und H (0|0|0). | 1) Betrachtet wird der abgebildete Würfel ABCDEFGH. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: D(0|0|-2),E(2|0|0), F(2|2|0) und H (0|0|0). | ||
| + | |||
| + | [[Bild:ABI2016_GI_TeilA_1.png|center|350px]] | ||
| + | |||
| + | a) Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen | ||
| + | Sie diese. Geben Sie die Koordinaten des Punkts A an. | ||
| + | |||
| + | b)Der Punkt P liegt auf der Kante [FB] des Würfels und hat vom Punkt H | ||
| + | den Abstand 3. Berechnen Sie die Koordinaten des Punkts P. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 40: | Zeile 46: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| − | |||
| − | |||
| + | <tr><td width="800px" valign="top"> | ||
| − | + | ;Aufgabe 2 | |
| + | Gegeben sind die Punkte A(-2|1|4) und B(-4|0|6).<br /> | ||
| − | + | a) Bestimmen Sie die Koordinaten des Punkts C so, dass gilt: <math> \vec{CA} = 2\cdot \vec{AB} </math> <br /> | |
| − | + | b) Durch die Punkte A und B verläuft die Gerade g. | |
| − | + | Betrachtet werden Geraden, für welche die Bedingungen I und II gelten: | |
| − | + | : I Jede dieser Geraden schneidet die Gerade g orthogonal. | |
| − | + | : II Der Abstand jeder dieser Geraden vom Punkt A beträgt 3 <br> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | Ermitteln Sie eine Gleichung für eine dieser Geraden. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | |||
| − | + | [[Bild:ABI2016_GI_TeilA_2ab_Lös.jpg|700px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
}} | }} | ||
Aktuelle Version vom 28. März 2018, 14:47 Uhr
|
|
1) Betrachtet wird der abgebildete Würfel ABCDEFGH. Die Eckpunkte D, E, F und H dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: D(0|0|-2),E(2|0|0), F(2|2|0) und H (0|0|0). a) Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen Sie diese. Geben Sie die Koordinaten des Punkts A an. b)Der Punkt P liegt auf der Kante [FB] des Würfels und hat vom Punkt H den Abstand 3. Berechnen Sie die Koordinaten des Punkts P.
|
Gegeben sind die Punkte A(-2|1|4) und B(-4|0|6). a) Bestimmen Sie die Koordinaten des Punkts C so, dass gilt: b) Durch die Punkte A und B verläuft die Gerade g. Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:
Ermitteln Sie eine Gleichung für eine dieser Geraden. |