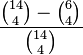Abi 2016 Stochastik II Teil A: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“)
 
 
(4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 22: Zeile 22:
  
 
;Aufgabe 1
 
;Aufgabe 1
−
 
+
Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl (Z) oder zum zweiten Mal Wappen (W) oben liegt. Als Ergebnismenge wird festgelegt: {ZZ; WW; ZWZ; ZWW; WZZ; WZW}.<br/>
 +
<br/>
 +
a) Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.<br/>
 +
<br/>
 +
b) Die Zufallsgröße X ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von X.   
  
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
Zeile 41: Zeile 45:
  
 
;Aufgabe 2
 
;Aufgabe 2
 +
An einem P-Seminar nehmen acht Mädchen und sechs Jungen teil, darunter
 +
Anna und Tobias. Für eine Präsentation wird per Los aus den Teilnehme-
 +
rinnen und Teilnehmern ein Team aus
 +
vier Personen zusammengestellt. <br/>
 +
a) Geben Sie zu jedem der folgenden Ereignisse einen Term an, mit dem
 +
die Wahrscheinlichkeit des Ereignisses berechnet werden kann.<br/>
 +
: A: „Anna und Tobias gehören dem Team an.“ <br />
 +
: B: „Das Team besteht aus gleich vielen Mädchen und Jungen.“ <br/>
 +
b) Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann:
  
−
 
+
:: <math>\frac{\binom{14}{4}-\binom{6}{4}}{\binom{14}{4}}</math>
  
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=

Aktuelle Version vom 27. März 2018, 20:46 Uhr


Mathematik (Bayern): Abiturprüfung 2016
Stochastik II - Teil A


Download der Originalaufgaben - Lösung zum Ausdrucken


Aufgabe 1

Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl (Z) oder zum zweiten Mal Wappen (W) oben liegt. Als Ergebnismenge wird festgelegt: {ZZ; WW; ZWZ; ZWW; WZZ; WZW}.

a) Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.

b) Die Zufallsgröße X ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von X.

700px



Aufgabe 2

An einem P-Seminar nehmen acht Mädchen und sechs Jungen teil, darunter Anna und Tobias. Für eine Präsentation wird per Los aus den Teilnehme- rinnen und Teilnehmern ein Team aus vier Personen zusammengestellt.
a) Geben Sie zu jedem der folgenden Ereignisse einen Term an, mit dem die Wahrscheinlichkeit des Ereignisses berechnet werden kann.

A: „Anna und Tobias gehören dem Team an.“
B: „Das Team besteht aus gleich vielen Mädchen und Jungen.“

b) Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit durch den folgenden Term berechnet werden kann:

\frac{\binom{14}{4}-\binom{6}{4}}{\binom{14}{4}}
700px


Von „http://rmg.zum.de/index.php?title=Abitur_Mathematik/Abi_2016_Stochastik_II_Teil_A&oldid=72034“