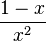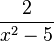Abi 2015 Analysis II Teil B: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | <center><big>'''Mathematik (Bayern): Abiturprüfung | + | <center><big>'''Mathematik (Bayern): Abiturprüfung 2015'''</big></center> |
<center><big>'''Analysis II - Teil B'''</big></center> | <center><big>'''Analysis II - Teil B'''</big></center> | ||
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | + | Der Graph G<sub>f</sub> einer in IR definierten Funktion <math>f : x \mapsto ax^4+bx^3</math>mit a,b ∈ IR besitzt im Punkt O(0|0) einen Wendepunkt mit waagrechter Tangente. | |
| − | |||
| − | + | a) W (1|1) ist ein weiterer Wendepunkt von G<sub>f</sub>. Bestimmen Sie mithilfe dieser Information die Werte von a und b. | |
| + | ''(Ergebnis: a = 1, b = -2)'' | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_1a_Lös.jpg|700px]] | ||
| + | }} | ||
| − | b) | + | b) |
| − | + | :{{Lösung versteckt|1= | |
| + | [[Bild:ABI2015_AII_TeilB_1b_Lös.jpg|700px]] | ||
| + | }} | ||
| − | + | c) | |
| + | Zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse G<sub>f</sub> sowie die Gerade g in ein Koordinatensystem ein. Ge | ||
| + | ben Sie die Gleichung der Geraden g an. | ||
| + | <math>\frac{1-x}{x^2}</math> | ||
| + | <math> </math> | ||
| + | <math>\frac{2}{x^2-5}</math> | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_1c_Lös.jpg|700px]] | ||
| + | }} | ||
| − | + | d) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | d) | + | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | + | [[Bild:ABI2015_AII_TeilB_1d_Lös.jpg|700px]] | |
| − | [[Bild: | + | |
| − | + | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 65: | Zeile 65: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | + | a) | |
| + | [[Bild:ABI2015_AII_TeilB_2a.jpg|center|350px]] | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_2a_Lös.jpg|700px]] | ||
| + | }} | ||
| + | b) | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | + | [[Bild:ABI2015_AII_TeilB_2b_Lös.jpg|700px]] | |
| − | [[Bild: | + | |
| − | + | ||
}} | }} | ||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
| Zeile 84: | Zeile 86: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| + | [[Bild:ABI2015_AII_TeilB_3.jpg|center|350px]] | ||
| + | a) | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_3a_Lös.jpg|700px]] | ||
| + | }} | ||
| + | b) | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_3b_Lös.jpg|700px]] | ||
| + | }} | ||
| − | [[Bild: | + | c) |
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_3c_Lös.jpg|700px]] | ||
| + | }} | ||
| + | d) | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:ABI2015_AII_TeilB_3d_Lös.jpg|700px]] | ||
}} | }} | ||
| − | + | e) | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | + | [[Bild:ABI2015_AII_TeilB_3e_Lös.jpg|700px]] | |
| − | [[Bild: | + | |
| − | + | ||
}} | }} | ||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
</div> | </div> | ||
Aktuelle Version vom 26. Juli 2017, 08:13 Uhr
|
|
Der Graph Gf einer in IR definierten Funktion
(Ergebnis: a = 1, b = -2) b) c)
Zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse Gf sowie die Gerade g in ein Koordinatensystem ein. Ge
ben Sie die Gleichung der Geraden g an.
d) |
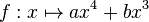 mit a,b ∈ IR besitzt im Punkt O(0|0) einen Wendepunkt mit waagrechter Tangente.
mit a,b ∈ IR besitzt im Punkt O(0|0) einen Wendepunkt mit waagrechter Tangente.