Abi 2015 Analysis I Teil B: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 39: | Zeile 39: | ||
Für x ∈ D<sub>f</sub> gilt <math>f(x)=\frac{1}{p(x)}</math>. | Für x ∈ D<sub>f</sub> gilt <math>f(x)=\frac{1}{p(x)}</math>. | ||
| + | [[Bild:ABI2015_AI_TeilA_1b.jpg|center|350px]] | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | [[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] | ||
| Zeile 69: | Zeile 70: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Gegeben ist die Funktion <math> h(x)= \frac{3}{e^{x+1} -1}</math> mit Definitionsbereich D<sub>h</sub> = ]-1;+∞[. Abbildung 2 zeigt den Graph G<sub>h</sub> von h. | ||
| + | [[Bild:ABI2015_AI_TeilA_2.jpg|center|350px]] | ||
| + | |||
a) | a) | ||
| + | Begründen Sie anhand des Funktionsterms, dass <math>\lim_{x\to\infty}h(x)= 0</math> gilt. Zeigen Sie rechnerisch für x ∈ D<sub>h</sub>, dass für die Ableitung h′ von h gilt: h′(x)<0. | ||
| + | Gegeben ist ferner die in D<sub>h</sub> definierte Integralfunktion '''H<sub>0</sub>:'''<math>\int_{x}^{0} h (t)\,dt</math> . | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_2a_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_2a_Lös.jpg|700px]] | ||
| Zeile 75: | Zeile 82: | ||
b) | b) | ||
| + | Begründen Sie ohne weitere Rechnung, dass folgende Aussagen wahr sind: | ||
| + | |||
| + | :α) Der Graph von H<sub>0</sub> ist streng monoton steigend. | ||
| + | |||
| + | :β) Der Graph von H<sub>0</sub> ist rechtsgekrümmt. | ||
| + | |||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_2b_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_2b_Lös.jpg|700px]] | ||
| Zeile 80: | Zeile 94: | ||
c) | c) | ||
| + | Geben Sie die Nullstelle von H<sub>0</sub> an und bestimmen Sie näherungsweise mithilfe von Abbildung 2 die Funktionswerte H<sub>0</sub> (-0,5) sowie H<sub>0</sub> (3). Skizzieren Sie in Abbildung 2 den Graphen von H<sub>0</sub> im Bereich -0,5 ≤ x ≤ 3. | ||
| + | |||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_2c_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_2c_Lös.jpg|700px]] | ||
| Zeile 97: | Zeile 114: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| + | In einem Labor wird ein Verfahren zur Reinigung von mit Schadstoffen kontaminiertem Wasser getestet. Die Funktion h aus Aufgabe 2 beschreibt für x ≥ 0 modellhaft die zeitliche Entwicklung des momentanen Schadstoffabbaus in einer bestimmten Wassermenge. Dabei bezeichnet h(x) die momentane Schadstoffabbaurate in Gramm pro Minute und x die seit Beginn des Reinigungsvorgangs | ||
| + | ergangene Zeit in Minuten. | ||
| + | |||
a) | a) | ||
| + | Bestimmen Sie auf der Grundlage des Modells den Zeitpunkt x, zu dem die momentane Schadstoffabbaurate auf 0,01 Gramm pro Minute zurückgegangen ist. Die in IR \ { -3; -1 } definierte Funktion <math> k(x) = 3 \cdot (\frac{1}{x+1} - \frac{1}{x+3}) -0,2 </math> stellt im Bereich -0,5 ≤ x ≤ 2 eine gute Näherung für die Funktion h dar. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_3a_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_3a_Lös.jpg|700px]] | ||
| Zeile 103: | Zeile 125: | ||
b) | b) | ||
| + | Beschreiben Sie, wie der Graph der Funktion k aus dem Graphen der Funktion f aus Aufgabe 1 hervorgeht. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_3b_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_3b_Lös.jpg|700px]] | ||
| Zeile 108: | Zeile 132: | ||
c) | c) | ||
| + | Berechnen Sie einen Näherungswert für <math>\int_{0}^{1} h (x)\,dx</math>, indem Sie den Zusammenhang <math>\int_{0}^{1} h (x)\,dx</math> '''≈''' <math>\int_{0}^{1} k (x)\,dx</math> verwenden. Geben Sie die Bedeutung dieses Werts im Sachzusammenhang an. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_3c_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_3c_Lös.jpg|700px]] | ||
Aktuelle Version vom 27. Juli 2017, 14:55 Uhr
|
|
Gegeben ist die Funktion f mit
b) Begründen Sie, dass die x-Achse horizontale Asymptote von Gf ist, und geben Sie die Gleichungen der vertikalen Asymptoten von Gf an. Be-
stimmen Sie die Koordinaten des Schnittpunkts von Gf mit der y-Achse. Abbildung 1 zeigt den Graphen der in IR definierten Funktion Für x ∈ Df gilt c) Gemäß der Quotientenregel gilt für die Ableitungen f' und p' die Beziehung: Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x = -2 einzige Nullstelle von f' ist und dass Gf in ]-3; -2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von Gf an. d) Berechnen Sie f(-5) und f(-1,5) und skizzieren sie Gf unter Berücksichtigung der Ergebnisse in Abbildung 1. |
Gegeben ist die Funktion a)
Begründen Sie anhand des Funktionsterms, dass b) Begründen Sie ohne weitere Rechnung, dass folgende Aussagen wahr sind:
c) Geben Sie die Nullstelle von H0 an und bestimmen Sie näherungsweise mithilfe von Abbildung 2 die Funktionswerte H0 (-0,5) sowie H0 (3). Skizzieren Sie in Abbildung 2 den Graphen von H0 im Bereich -0,5 ≤ x ≤ 3.
|
In einem Labor wird ein Verfahren zur Reinigung von mit Schadstoffen kontaminiertem Wasser getestet. Die Funktion h aus Aufgabe 2 beschreibt für x ≥ 0 modellhaft die zeitliche Entwicklung des momentanen Schadstoffabbaus in einer bestimmten Wassermenge. Dabei bezeichnet h(x) die momentane Schadstoffabbaurate in Gramm pro Minute und x die seit Beginn des Reinigungsvorgangs ergangene Zeit in Minuten. a)
Bestimmen Sie auf der Grundlage des Modells den Zeitpunkt x, zu dem die momentane Schadstoffabbaurate auf 0,01 Gramm pro Minute zurückgegangen ist. Die in IR \ { -3; -1 } definierte Funktion b) Beschreiben Sie, wie der Graph der Funktion k aus dem Graphen der Funktion f aus Aufgabe 1 hervorgeht. c)
Berechnen Sie einen Näherungswert für
|
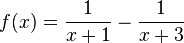 und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
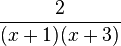 ;
;
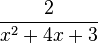 ;
;
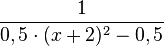

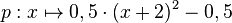 , die die Nullstellen x = -3 und x = -1 hat.
, die die Nullstellen x = -3 und x = -1 hat.
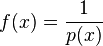 .
.

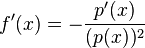 für x ∈ Df.
für x ∈ Df.


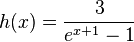 mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
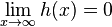 gilt. Zeigen Sie rechnerisch für x ∈ Dh, dass für die Ableitung h′ von h gilt: h′(x)<0.
Gegeben ist ferner die in Dh definierte Integralfunktion H0:
gilt. Zeigen Sie rechnerisch für x ∈ Dh, dass für die Ableitung h′ von h gilt: h′(x)<0.
Gegeben ist ferner die in Dh definierte Integralfunktion H0: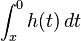 .
.
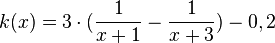 stellt im Bereich -0,5 ≤ x ≤ 2 eine gute Näherung für die Funktion h dar.
stellt im Bereich -0,5 ≤ x ≤ 2 eine gute Näherung für die Funktion h dar.
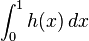 , indem Sie den Zusammenhang
, indem Sie den Zusammenhang 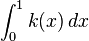 verwenden. Geben Sie die Bedeutung dieses Werts im Sachzusammenhang an.
verwenden. Geben Sie die Bedeutung dieses Werts im Sachzusammenhang an.

