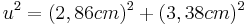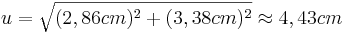Satz des Pythagoras: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Wenn du fertig bist, dann hole dir vorne ein Arbeitsblatt mit weiteren Übungen ab!)
 
(7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 7: Zeile 7:
 
Der Radfahrer hat die Möglichkeit, den Radweg übers Feld zu nehmen, oder auf der Straße zu bleiben.
 
Der Radfahrer hat die Möglichkeit, den Radweg übers Feld zu nehmen, oder auf der Straße zu bleiben.
 
Es stellt sich die Frage: Ist der Feldweg eine Abkürzung? Wie lang ist die Strecke a?
 
Es stellt sich die Frage: Ist der Feldweg eine Abkürzung? Wie lang ist die Strecke a?
 +
 +
  
 
Im Folgenden wirst du kennenlernen, wie man eine solche Streckenlänge berechnen kann.
 
Im Folgenden wirst du kennenlernen, wie man eine solche Streckenlänge berechnen kann.
 +
 +
  
 
Hol dir dazu vorne das Kuvert mit dem beiliegenden Zettel.
 
Hol dir dazu vorne das Kuvert mit dem beiliegenden Zettel.
Zeile 31: Zeile 35:
  
  
−
[[Hier geht es nun zum Hefteintrag]]
+
<popup name="Quadrat 1">A_1=(a+b)<sup>2</sup> = a<sup>2</sup> +2ab+b<sup>2</sup></popup>
 +
 
 +
<popup name="Quadrat 2">A_2=c<sup>2</sup> +4(0,5ab)=c<sup>2</sup> + 2ab</popup>
 +
 
 +
 
 +
Setze nun beide Terme gleich und vereinfache die Gleichung!
 +
 
 +
 
 +
Bringe nun das Kuvert vollständig wieder nach vorne und nimm dir den Beweis mit!
 +
 
 +
 
 +
----
 +
 
 +
 
 +
[[9d 2014 15/Satz des Pythagoras/Hefteintrag|Hier geht es nun zum Hefteintrag]]
  
  
  
 
Da es für unser Ausgangsproblem nötig ist, die Länge der Hypotenuse zu bestimmen, müssen wir die Formel umformen!
 
Da es für unser Ausgangsproblem nötig ist, die Länge der Hypotenuse zu bestimmen, müssen wir die Formel umformen!
−
[[Hier erarbeitest du Ergänzungen dazu]]
+
[[9d 2014 15/Satz des Pythagoras/Ergänzungen|Hier erarbeitest du Ergänzungen]]
  
  
Zeile 42: Zeile 60:
  
 
==Hier geht es zu einer interaktiven Übung:==
 
==Hier geht es zu einer interaktiven Übung:==
−
[[http://learningapps.org/239105]]!=
+
[http://learningapps.org/239105]
  
  
Zeile 62: Zeile 80:
 
|}
 
|}
  
−
----
 
  
−
{| width="90%"
 
−
|width="30%" style="vertical-align:top" |
 
−
[[Bild:Aufgabe zum Satz des Pythagoras 1.png]]
 
−
 
−
| width="1%" style="vertical-align:top" |
 
−
 
−
| width="50%" style="vertical-align:top" |
 
−
{{Lösung versteckt|
 
−
*Das Dreieck ist nicht rechtwinklig, da der fehlende Winkel 89,97° beträgt
 
−
*Man kann den Satz des Pythagoras also nicht anwenden da es sich um kein rechtwinkliges Dreieck handelt
 
−
}}
 
−
|}
 
  
 
----
 
----
Zeile 107: Zeile 112:
 
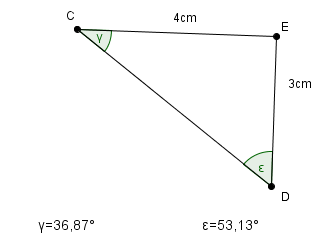
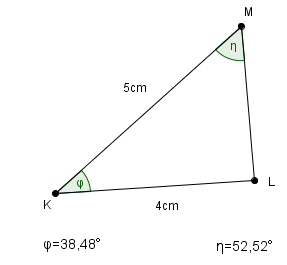
*Die Hypotenuse (u) ist etwa 4,43cm lang}}
 
*Die Hypotenuse (u) ist etwa 4,43cm lang}}
 
|}<br />
 
|}<br />
 +
 +
----
 +
 +
===Wenn du fertig bist, dann hole dir vorne ein Arbeitsblatt mit weiteren Übungen ab!===
 +
 +
Lösungen kannst du hier abrufen:
 +
[[Lösungen Arbeitsblatt Pythagoras]]

Aktuelle Version vom 24. November 2014, 11:10 Uhr

Satz des Pythagoras

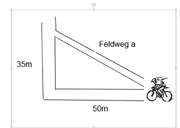
Auf dem nebenstehenden Bild seht ihr einen Weg, der eine Abzweigung im rechten Winkel aufweist.

Problem des Fahrradfahrers

Der Radfahrer hat die Möglichkeit, den Radweg übers Feld zu nehmen, oder auf der Straße zu bleiben. Es stellt sich die Frage: Ist der Feldweg eine Abkürzung? Wie lang ist die Strecke a?


Im Folgenden wirst du kennenlernen, wie man eine solche Streckenlänge berechnen kann.


Hol dir dazu vorne das Kuvert mit dem beiliegenden Zettel.

Arbeitsauftrag: Lege mit den gegebenen Formen die beiden Quadrate auf dem Arbeitsblatt vollständig aus!


Wenn du nicht weiterkommst, dann helfen dir die Tipps!


Arbeitsauftrag: Fülle nun die darunter stehenden Flächenvergleiche aus, indem du die benötigten Puzzelstücke addierst und anschließend den so erhaltenen Term vereinfachst!

Setze anschließend beide Terme gleich und vereinfache erneut!



Setze nun beide Terme gleich und vereinfache die Gleichung!


Bringe nun das Kuvert vollständig wieder nach vorne und nimm dir den Beweis mit!



Hier geht es nun zum Hefteintrag


Da es für unser Ausgangsproblem nötig ist, die Länge der Hypotenuse zu bestimmen, müssen wir die Formel umformen! Hier erarbeitest du Ergänzungen


Jetzt kannst du schon die den Satz des Pythagoras anwenden!

Hier geht es zu einer interaktiven Übung:

[1]


Aufgaben zum Berechnen

Aufgabe zum Satz des Pythagoras Beispiel.png

  • Es handelt sich um ein rechtwinkliges Dreieck, da 180° - 36,87° - 53,13° = 90°
  • Kathete1 (c) ist 3cm und Kathete2 (d) ist 4cm lang
  • Die Hypotenuse (e) ist gesucht
  • {e^2=3^2+4^2\,}
  • {e^2=25\,}
  • e=\sqrt{25}=5
  • Die Hypotenuse ist 5cm lang


Aufgabe zum Satz des Pythagoras 3.png

  • Es handelt sich um kein rechtwinkliges Dreieck, da der dritte Winkel im Dreieck 89° beträgt
  • Der Satz des Pythagoras kann also nicht angewendet werden, da nur eine Verwendung in rechtwinkligen Dreiecken möglich ist

Aufgabe zum Satz des Pythagoras 2.png

  • Es handelt sich um ein rechtwinkliges Dreieck
  • Die Hypotenuse (u) wird gesucht, Kathete1 (w) ist 2,86cm und Kathete2 (v) ist 3,38cm lang
  • {u^2=(2,86cm)^2+(3,38cm)^2\,}
  • u=\sqrt{(2,86cm)^2+(3,38cm)^2}\approx4,43cm
  • Die Hypotenuse (u) ist etwa 4,43cm lang

Wenn du fertig bist, dann hole dir vorne ein Arbeitsblatt mit weiteren Übungen ab!

Lösungen kannst du hier abrufen: Lösungen Arbeitsblatt Pythagoras

Von „http://rmg.zum.de/index.php?title=9d_2014_15/Satz_des_Pythagoras&oldid=60769“