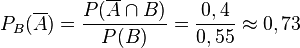Stochastik: Unterschied zwischen den Versionen
(→Teste dein Wissen) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
<div style="background: #ABAABF"> | <div style="background: #ABAABF"> | ||
| + | |||
| + | |||
| + | |||
<center><table border=0 width="800px" cellpadding=5 cellspacing=5> | <center><table border=0 width="800px" cellpadding=5 cellspacing=5> | ||
| Zeile 60: | Zeile 63: | ||
| <math> \overline{B} </math> || '''0,05''' || '''0,4''' || '''0,45''' | | <math> \overline{B} </math> || '''0,05''' || '''0,4''' || '''0,45''' | ||
|- | |- | ||
| − | | || 0,2 || '''0, | + | | || 0,2 || '''0,8''' || '''1''' |
|} | |} | ||
</popup> | </popup> | ||
| Zeile 94: | Zeile 97: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | |||
</div> | </div> | ||
Aktuelle Version vom 12. September 2014, 15:47 Uhr
|
|

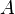
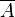
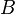
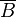
 B ein
B ein
 B ein
B ein