Geometrie: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
<div style="background: #ABAABF"> | <div style="background: #ABAABF"> | ||
| + | |||
| + | |||
| + | |||
<center><table border=0 width="800px" cellpadding=5 cellspacing=5> | <center><table border=0 width="800px" cellpadding=5 cellspacing=5> | ||
| Zeile 45: | Zeile 48: | ||
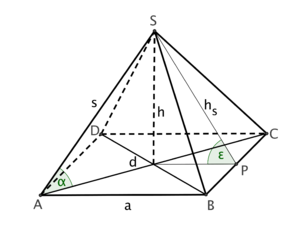
<math> (\frac a2)^2 + h^2 = h_s^2 </math> <br/> | <math> (\frac a2)^2 + h^2 = h_s^2 </math> <br/> | ||
da h=2a folgt: <math> (\frac a2)^2 + (2a)^2 = h_s^2 </math> <br/> | da h=2a folgt: <math> (\frac a2)^2 + (2a)^2 = h_s^2 </math> <br/> | ||
| − | somit folgt: <math> h_s=\ | + | somit folgt: <math> h_s=\sqrt{4,25} a</math> |
</popup> | </popup> | ||
c) Gib an, welche der folgenden Beziehungen richtig sind. | c) Gib an, welche der folgenden Beziehungen richtig sind. | ||
| Zeile 77: | Zeile 80: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | |||
</div> | </div> | ||
Aktuelle Version vom 12. September 2014, 15:48 Uhr
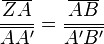 )
( In Figur 1 gilt:
)
( In Figur 1 gilt: 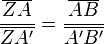 )
)
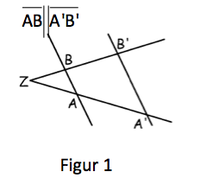

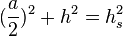
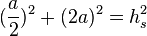
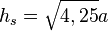
 )
(!
)
(! 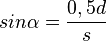 )
(!
)
(! 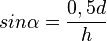 )
)
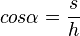 )
(!
)
(! 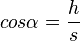 )
(
)
( 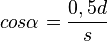 )
)
 )
(
)
( 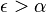 )
(!
)
(! 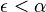 )
)




