Geometrie: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
<div style="background: #ABAABF"> | <div style="background: #ABAABF"> | ||
| + | |||
| + | |||
| + | |||
<center><table border=0 width="800px" cellpadding=5 cellspacing=5> | <center><table border=0 width="800px" cellpadding=5 cellspacing=5> | ||
| Zeile 10: | Zeile 13: | ||
<br/> | <br/> | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | 1) Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Kreuze die | + | '''1) Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Kreuze die korrekten Aussagen an.''' |
| − | (! Für ein Parallelogramm | + | (! Für ein Parallelogramm mit den Seitenlängen a=4cm, b=3 cm gilt stets A=12cm<sup>2</sup>.) |
(Ein achsensymmetrisches Trapez mit einem 90° Winkel ist ein Rechteck.) | (Ein achsensymmetrisches Trapez mit einem 90° Winkel ist ein Rechteck.) | ||
(Jedes gleichseitige Dreieck ist ein gleichschenkliges Dreieck.) | (Jedes gleichseitige Dreieck ist ein gleichschenkliges Dreieck.) | ||
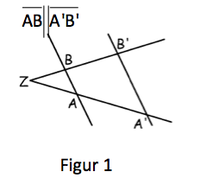
| + | (! In Figur 1 gilt: <math> \frac {\overline{ZA}} {\overline{AA'}} = \frac {\overline{AB}} {\overline{A'B'}} </math> ) | ||
| + | ( In Figur 1 gilt: <math> \frac {\overline{ZA}} {\overline{ZA'}} = \frac {\overline{AB}} {\overline{A'B'}} </math> ) | ||
</div> | </div> | ||
| − | + | [[Datei:StrahlensatzTesteDeinWissen.png|200px]] | |
|width="5%"| | |width="5%"| | ||
|valign="top"| | |valign="top"| | ||
| + | |||
| + | |||
== Knicktests == | == Knicktests == | ||
<br/> | <br/> | ||
| + | [[Datei:5AB 1 Viereck Dreieck Strahlensatz.pdf|thumb|Knicktest - Vierecke,Dreiecke,Strahlensatz]] | ||
|} | |} | ||
| + | |||
| + | {| | ||
| + | |width="70%"| | ||
| + | <br/> | ||
| + | <br/> | ||
| + | |||
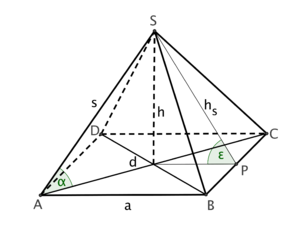
| + | '''2) Betrachte eine gerade Pyramide mit quadratischer Grundfläche (Seitenlänge a) und einer Höhe von 2a.''' <br/> | ||
| + | [[Datei:TesteDeinWissen Pyramide.png|Pyramide - Teste dein Wissen Geometrie|300px]] | ||
| + | <br/> | ||
| + | a) Gib das Volumen in Abhängigkeit von a an. | ||
| + | <popup name="Lösung"> | ||
| + | Das Volumen eines Spitzkörpers berechnet man mit V=⅓G·h=⅓·a·a·2a=⅔a<sup>3</sup> | ||
| + | </popup> | ||
| + | |||
| + | b) Stelle eine Gleichung zur Berechnung von h<sub>s</sub> in Abhängigkeit von a auf. | ||
| + | <popup name="Lösung"> | ||
| + | Mit dem "Satz des Pythagoras" folgt: | ||
| + | <math> (\frac a2)^2 + h^2 = h_s^2 </math> <br/> | ||
| + | da h=2a folgt: <math> (\frac a2)^2 + (2a)^2 = h_s^2 </math> <br/> | ||
| + | somit folgt: <math> h_s=\sqrt{4,25} a</math> | ||
| + | </popup> | ||
| + | c) Gib an, welche der folgenden Beziehungen richtig sind. | ||
| + | <div class="multiplechoice-quiz"> | ||
| + | ( <math> sin \alpha = \frac h s </math> ) | ||
| + | (! <math> sin \alpha = \frac {0,5d} {s} </math> ) | ||
| + | (! <math> sin \alpha = \frac {0,5d} {h} </math> ) | ||
| + | |||
| + | (! <math> cos \alpha = \frac s h </math> ) | ||
| + | (! <math> cos \alpha = \frac h s </math> ) | ||
| + | ( <math> cos \alpha = \frac {0,5d} {s} </math> ) | ||
| + | |||
| + | (! <math> \epsilon = \alpha </math> ) | ||
| + | ( <math> \epsilon > \alpha </math> ) | ||
| + | (! <math> \epsilon < \alpha </math> ) | ||
| + | </div> | ||
| + | |||
| + | |width="5%"| | ||
| + | |valign="top"| | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | <br/> | ||
| + | |||
| + | [[Datei:5AB 2 Pythagoras Trigonom.pdf|thumb|Knicktest - Satz des Pythagoras, Trigonometrie]]<br/> | ||
| + | [[Datei:5AB 3 Flächen.pdf|thumb|Knicktest - Flächenberechnung]]<br/> | ||
| + | [[Datei:5AB 4 Volumen.pdf|thumb|Knicktest - Volumenberechnung]] | ||
| + | |} | ||
| + | |||
[[Mathematik_Grundwissen_10|Zurück zur Übersicht]] | [[Mathematik_Grundwissen_10|Zurück zur Übersicht]] | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | |||
</div> | </div> | ||
Aktuelle Version vom 12. September 2014, 15:48 Uhr
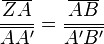 )
( In Figur 1 gilt:
)
( In Figur 1 gilt: 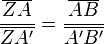 )
)

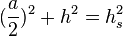
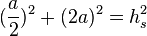
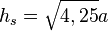
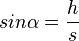 )
(!
)
(! 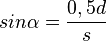 )
(!
)
(! 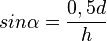 )
)
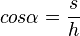 )
(!
)
(! 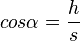 )
(
)
( 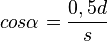 )
)
 )
(
)
( 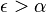 )
(!
)
(! 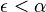 )
)




