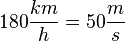Geschwindigkeit: Unterschied zwischen den Versionen
Aus RMG-Wiki
K |
K |
||
| (33 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0px; margin-right:95px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:lightblue; width:90%; align:center; "> | ||
{{Lernpfad Mechanik}} | {{Lernpfad Mechanik}} | ||
| − | + | '''<span style="color: blue"><big>Einführung:</big></span>''' | |
| − | + | {|width="100%" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | '''<span style="color: blue">Einführung:</span>''' | + | |
| − | {|width=" | + | |
|width="40%" style="vertical-align:top"| | |width="40%" style="vertical-align:top"| | ||
| − | Geschwindigkeit''' <br /> | + | '''<u>Geschwindigkeit</u>''' <br /> |
Ein großes Teilgebiet der Mechanik ist die Kinematik (den Wortteil "Kin" kennst du aus dem Kino: dort werden Bilder bewegt. Kinematik bedeutet also Bewegung.). <br /> | Ein großes Teilgebiet der Mechanik ist die Kinematik (den Wortteil "Kin" kennst du aus dem Kino: dort werden Bilder bewegt. Kinematik bedeutet also Bewegung.). <br /> | ||
Fangen wir direkt mit der einfachsten Art der Fortbewegung an: <br /> | Fangen wir direkt mit der einfachsten Art der Fortbewegung an: <br /> | ||
| Zeile 16: | Zeile 11: | ||
<br /> | <br /> | ||
Ein Beispiel aus dem Alltag: <br /> | Ein Beispiel aus dem Alltag: <br /> | ||
| − | Deine Schulklasse wandert 12km in | + | Deine Schulklasse wandert 12km in 3 Stunden. Du möchtest nun wissen wie schnell ihr im Durchschnitt wart. Wie groß wäre nun die Geschwindigkeit in <math> \frac{km}{h} </math> ? <br /> |
<popup name="Lösung"> | <popup name="Lösung"> | ||
Richtig! Natürlich ist die Antwort 4 <math> \frac{km}{h} </math> | Richtig! Natürlich ist die Antwort 4 <math> \frac{km}{h} </math> | ||
| Zeile 23: | Zeile 18: | ||
Du siehst einen 100m-Sprint bei den Olympischen Spielen. Der Sieger hat eine Zeit von genau 10s. Er hat also 100m in 10s zurückgelegt. Welche durchschnittliche Geschwindigkeit hatte der Sprinter? <br /> | Du siehst einen 100m-Sprint bei den Olympischen Spielen. Der Sieger hat eine Zeit von genau 10s. Er hat also 100m in 10s zurückgelegt. Welche durchschnittliche Geschwindigkeit hatte der Sprinter? <br /> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | Hier sollte es dir nicht mehr so leicht fallen die Geschwindigkeit in Kilometer pro Stunde anzugeben. Einfacher wäre jetzt die Geschwindigkeit in Meter pro Sekunde, also <math> \frac{m}{s} </math> anzugeben. Das Erbebnis weißt du doch bestimmt! | + | Hier sollte es dir nicht mehr so leicht fallen die Geschwindigkeit in Kilometer pro Stunde anzugeben. Einfacher wäre jetzt die Geschwindigkeit in Meter pro Sekunde, also <math> \frac{m}{s} </math> anzugeben. Das Erbebnis weißt du doch bestimmt! (10 <math> \frac{m}{s} </math> ) |
</popup> <br /> | </popup> <br /> | ||
Also wie kann man nun die Geschwindigkeit berechnen? | Also wie kann man nun die Geschwindigkeit berechnen? | ||
| − | + | ''' <big>Bearbeite folgenden Lückentext:</big>''' | |
| − | Bearbeite folgenden Lückentext: | + | <span style="color:#C00000"> <div class="lueckentext-quiz"> |
| − | <div class="lueckentext-quiz"> | + | |
Möchte man die '''durchschnittliche''' Geschwindigkeit eines Körpers berechnen, so '''dividiert''' man die '''zurückgelegte Strecke''' durch die '''dafür benötigte Zeit'''. <br /> | Möchte man die '''durchschnittliche''' Geschwindigkeit eines Körpers berechnen, so '''dividiert''' man die '''zurückgelegte Strecke''' durch die '''dafür benötigte Zeit'''. <br /> | ||
Teilt man dabei eine Strecke in der Einheit '''Meter''' durch die Zeit in der Einheit '''Sekunde''' so erhält man folglich die Geschwindigkeit in der Einheit <math> {m \over s} </math> <br /> | Teilt man dabei eine Strecke in der Einheit '''Meter''' durch die Zeit in der Einheit '''Sekunde''' so erhält man folglich die Geschwindigkeit in der Einheit <math> {m \over s} </math> <br /> | ||
| − | </div> | + | </div> </span> |
| − | + | ||
<popup name="Hefteintrag!!"> | <popup name="Hefteintrag!!"> | ||
Übernehme den richtig ausgefüllten Lückentext mit der Überschrift: "Kinematik" und darunter "Geradlinige gleichförmige Bewegung" in dein Heft. <br /> | Übernehme den richtig ausgefüllten Lückentext mit der Überschrift: "Kinematik" und darunter "Geradlinige gleichförmige Bewegung" in dein Heft. <br /> | ||
| + | Außerdem soll alles, was in roter Farbe geschrieben ist, ebenfalls in dein Heft! (inklusive der Formeln innerhalb der Sätze!!) <br /> | ||
Die folgende Aufgabe sollst du ebenfalls in deinem Heft bearbeiten. Danach kannst du die Lösungen vergleichen. | Die folgende Aufgabe sollst du ebenfalls in deinem Heft bearbeiten. Danach kannst du die Lösungen vergleichen. | ||
| Zeile 44: | Zeile 38: | ||
<div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> | ||
| − | '''< | + | '''<big>Aufgabe 1: (ins Heft!)</big>''' |
a) Berechne mit Hilfe des Videos die durchschnittliche Geschwindigkeit des Pkws insgesamt. <br /> | a) Berechne mit Hilfe des Videos die durchschnittliche Geschwindigkeit des Pkws insgesamt. <br /> | ||
| Zeile 52: | Zeile 46: | ||
b) Berechne nun die durchschnittliche Geschwindigkeit des Pkws auf den ersten 6 Metern. <br /> | b) Berechne nun die durchschnittliche Geschwindigkeit des Pkws auf den ersten 6 Metern. <br /> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | Für die ersten 6m benötigt der Pkw 2, | + | Für die ersten 6m benötigt der Pkw etwa 2,4s. Wir berechnen wieder die Geschwindigkeit mit der gleichen Formel, setzen aber diesmal andere Werte für s und t ein: <math> v = \frac{s}{t} = \frac{6m}{2,4s} = 2,5\frac{m}{s} </math> |
</popup> | </popup> | ||
c) Wie kannst du die Geschwindigkeit auf den letzten 6 Metern ausrechnen? Versuche eine allgemeine Formel anzugeben. <br /> | c) Wie kannst du die Geschwindigkeit auf den letzten 6 Metern ausrechnen? Versuche eine allgemeine Formel anzugeben. <br /> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
Da man immer den zurückgelegten Weg durch die dafür benötigte Zeit teilt, aber der gesuchte Wegabschnitt oder die gesuchte Zeit nicht immer bei Null beginnen, muss man jeweils die Differenz der Wegstrecke am Ende des gesuchten Zeitintervalls und der Wegstrecke am Anfang des gesuchten Zeitintervalls berechnen. Entsprechend muss man die Länge des Zeitintervalls angeben. <br /> | Da man immer den zurückgelegten Weg durch die dafür benötigte Zeit teilt, aber der gesuchte Wegabschnitt oder die gesuchte Zeit nicht immer bei Null beginnen, muss man jeweils die Differenz der Wegstrecke am Ende des gesuchten Zeitintervalls und der Wegstrecke am Anfang des gesuchten Zeitintervalls berechnen. Entsprechend muss man die Länge des Zeitintervalls angeben. <br /> | ||
| − | Die Formel zur Berechnung lautet: Geschwindigkeit [[bild:Bruch.jpg|150px]] oder <math>v = \frac{\Delta s}{\Delta t}</math> (Gesprochen: <math> \Delta </math> delta) <br /> | + | <span style="color:#C00000"> Die Formel zur Berechnung lautet: Geschwindigkeit = [[bild:Bruch.jpg|150px]] oder <math>v = \frac{\Delta s}{\Delta t}</math> (Gesprochen: <math> \Delta </math> delta) </span> <br /> |
Im Video ist zu erkennen, dass das Auto für die letzten 6m, also von der 6m bis zur 12m Markierung, insgesamt 4,80s-2,42s = 2,38s ≈ 2,4s gebraucht hat. Die Geschwindigkeit beträgt somit: <br /> | Im Video ist zu erkennen, dass das Auto für die letzten 6m, also von der 6m bis zur 12m Markierung, insgesamt 4,80s-2,42s = 2,38s ≈ 2,4s gebraucht hat. Die Geschwindigkeit beträgt somit: <br /> | ||
| − | <math>v = \frac{\Delta s}{\Delta t} = \frac{6m}{2, | + | <math>v = \frac{\Delta s}{\Delta t} = \frac{12m-6m}{4,80s-2,42s}</math> = <math> \frac{6m}{2,38s}</math> ≈ <math> 2,5 \frac{m}{s} </math> |
</popup> | </popup> | ||
{{#ev:youtube |BTiaZqhtjjc|350}} | {{#ev:youtube |BTiaZqhtjjc|350}} | ||
| + | <br /> | ||
| + | <popup name="Wichtiger Hinweis für Schulaufgaben!!"> | ||
| + | Es ist sehr wichtig, dass jeder gut nachvollziehen kannst, was du gerade berechnest und wie du das tust. <br /> | ||
| + | Deshalb halte dich an folgende Form! Schreibe immer auf, was du gerade berechnest, also bei Aufgabe 1c) wäre das zum Beispiel: "Berechne die durchschnittliche Geschwindigkeit zwischen der 6m und der 12m Markierung." Danach muss die physikalische Formel, die eingesetzten Werte und das Ergebnis (richtig gerundet!) folgen: <br /> | ||
| + | <math>v = \frac{\Delta s}{\Delta t} = \frac{12m-6m}{4,80s-2,42s}</math> = <math> \frac{6m}{2,4s} </math> ≈ <math> 2,5 \frac{m}{s} </math> <br /> | ||
| + | Entweder sollte das Ergebnis unterstrichen werden oder ein Antwortsatz folgen. Wichtig ist, dass die Einheiten beim Endergebnis und auch in der Rechnung stimmen! | ||
| + | </popup> | ||
| − | + | <span style="color:#C00000"> "<math> \Delta </math> s" bedeutet "Streckenabschnitt am Ende" minus "Streckenabschnitt am Anfang" des betrachteten Zeitintervalls.</span> (Das ist wichtig, wenn wir wie in Aufgabe 1c) die Geschwindigkeit in den letzten 6 Metern der Bewegung des Pkws ausrechnen wollen: <br /> | |
| − | + | <math> \Delta </math> s = 12m-6m = 6m) <br /> | |
| − | "<math> \Delta </math> s" bedeutet "Streckenabschnitt am Ende" minus "Streckenabschnitt am Anfang". (Das ist wichtig, wenn wir | + | |
<br /> | <br /> | ||
| Zeile 81: | Zeile 81: | ||
Gehen wir von der 1. Darstellung in m/s aus: <br /> | Gehen wir von der 1. Darstellung in m/s aus: <br /> | ||
| − | <math> 1 {m \over s} = 1 \frac{\frac{1}{1000}km }{\frac{1}{3600}h } = {3600km \over 1000h} = 3,6 {km \over h} </math> | + | <span style="color:#C00000"> <math> 1 {m \over s} = 1 \frac{\frac{1}{1000}km }{\frac{1}{3600}h } = {3600km \over 1000h} = 3,6 {km \over h} </math> </span> <br /> |
| − | 1 Meter | + | <br /> |
| + | 1 Meter ist <math>{1 \over 1000}</math>km und 1 Sekunde ist <math>{1 \over 3600}h </math> (1h sind 60min mit jeweils 60s); am Ende noch durch den Bruch teilen <br /> | ||
<br /> | <br /> | ||
| − | Bei der Umrechnung von <math>{m \over s}</math> in <math>{km \over h}</math> muss man den Wert mit 3,6 multiplizieren und zusätzlich die Einheit ändern: Z.B. <math>20{m \over s} = 72{km \over h}</math> | + | <span style="color:#C00000"> Bei der Umrechnung von <math>{m \over s}</math> in <math>{km \over h}</math> muss man den Wert mit 3,6 multiplizieren und zusätzlich die Einheit ändern: Z.B. <math>20{m \over s} = 72{km \over h}</math> </span> <br /><br /> |
| − | + | ||
| − | Bei der Umrechnung von <math>{km \over h} in {m \over s}</math> muss man den Wert durch 3,6 teilen und anschließend die Einheit ändern: Z.B. <math>180{km \over h} = 50{m \over s}</math> | + | <span style="color:#C00000"> Bei der Umrechnung von <math>{km \over h} in {m \over s}</math> muss man den Wert durch 3,6 teilen und anschließend die Einheit ändern: Z.B. <math>180{km \over h} = 50{m \over s}</math> </span> <br /> <br /> |
| − | + | ||
| − | <big><span style="color:#C00000"> Faustformel: "Der kleinere Wert ist in <math>{m \over s}</math> und der Umrechnungsfaktor ist 3,6." | + | <big><span style="color:#C00000"> '''Faustformel: "Der kleinere Wert ist in <math>{m \over s}</math> und der Umrechnungsfaktor ist 3,6."</span> |
| − | Als nächstes kannst du mit folgendem Quiz das gerade Gelernte anwenden: [http://learningapps.org/413137 Quiz über Geschwindigkeiten] <br /> | + | Als nächstes kannst du mit folgendem Quiz das gerade Gelernte anwenden: Frage 1-6 (Frage 7-10 kannst du ebenfalls versuchen, diese beschäftigen sich jedoch schon mit dem neuen Thema): [http://learningapps.org/413137 Quiz über Geschwindigkeiten] <br /> |
<br /> | <br /> | ||
Damit du ein besseres Gefühl für Geschwindigkeiten bekommst, darfst du dich jetzt noch an folgende "learning-app" versuchen: | Damit du ein besseres Gefühl für Geschwindigkeiten bekommst, darfst du dich jetzt noch an folgende "learning-app" versuchen: | ||
[http://learningapps.org/16371 Schätzen von Geschwindigkeiten] | [http://learningapps.org/16371 Schätzen von Geschwindigkeiten] | ||
Aktuelle Version vom 4. März 2014, 21:36 Uhr
|
Einführung:
|
Geschwindigkeit Ein weiteres Beispiel: Also wie kann man nun die Geschwindigkeit berechnen? Bearbeite folgenden Lückentext: Möchte man die durchschnittliche Geschwindigkeit eines Körpers berechnen, so dividiert man die zurückgelegte Strecke durch die dafür benötigte Zeit. Aufgabe 1: (ins Heft!) a) Berechne mit Hilfe des Videos die durchschnittliche Geschwindigkeit des Pkws insgesamt. b) Berechne nun die durchschnittliche Geschwindigkeit des Pkws auf den ersten 6 Metern. c) Wie kannst du die Geschwindigkeit auf den letzten 6 Metern ausrechnen? Versuche eine allgemeine Formel anzugeben.
Umrechnung von Bei der Umrechnung von Bei der Umrechnung von Faustformel: "Der kleinere Wert ist in
|
? 
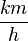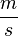anzugeben. Das Erbebnis weißt du doch bestimmt! (10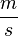 
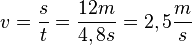
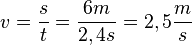
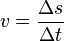(Gesprochen: 
delta)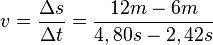 
= 
≈ 
≈ 
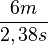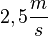
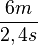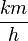und umgekehrt
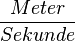oder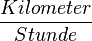 
In der Physik bietet sich meistens die 1. Darstellung an, während du im Alltag meistens mit der 2. Darstellung konfrontiert wirst.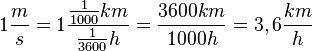 
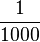km und 1 Sekunde ist 
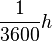(1h sind 60min mit jeweils 60s); am Ende noch durch den Bruch teilen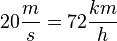 
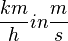muss man den Wert durch 3,6 teilen und anschließend die Einheit ändern: Z.B. 
