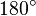Dreieck: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (13 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br><br> | <br><br> | ||
| − | =<span style="background:RoyalBlue1">Das | + | =<span style="background:RoyalBlue1">Das Dreieck</span>= |
{|width="95%" | {|width="95%" | ||
|width="20%" style="vertical-align:top"| | |width="20%" style="vertical-align:top"| | ||
| − | [[Bild:Bermuda-dreieck.png| | + | [[Bild:Bermuda-dreieck.png|300px]] |
|width="5%" style="vertical-align:top"| | |width="5%" style="vertical-align:top"| | ||
|width="55%" style="vertical-align:center"| | |width="55%" style="vertical-align:center"| | ||
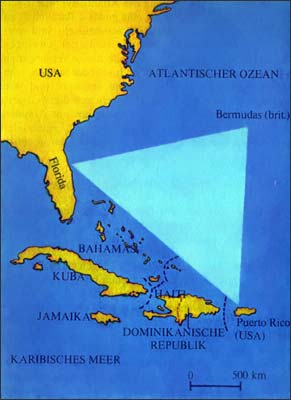
| − | Das Bermudadreieck ist die Bezeichnung für ein Seegebiet, das sich im westlichen Atlantik, nördlich der Karibik befindet. Schiffe | + | Das Bermudadreieck ist die Bezeichnung für ein Seegebiet, das sich im westlichen Atlantik, nördlich der Karibik befindet. Schiffe verschwinden bei besten Wetterbedingungen und ruhiger See spurlos oder treiben als verlassene, aber völlig intakte Geisterschiffe im Meer, während die Mannschaften verschollen bleiben. Schiffskapitäne versuchen dieses Bermudadreieck möglichst nicht zu befahren. |
| + | |||
| + | Wie groß ist nun die Fläche dieses "Dreiecks", das man besser meiden sollte? | ||
| + | |||
| + | Bald wirst du sie selbst berechnen können. | ||
|} | |} | ||
| − | ==Das | + | =<span style="background:RoyalBlue1">Das Dreieck</span>= |
{| | {| | ||
| − | |[[Bild: | + | |[[Bild:Open book nae 02.svg|200px]] |
|<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:80%; align:center; "> | |<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white; width:80%; align:center; "> | ||
<span style="color: green">'''Arbeitsauftrag:'''</span> | <span style="color: green">'''Arbeitsauftrag:'''</span> | ||
| − | *Zeiche das | + | *Zeiche das unten stehende Dreieck mit den gegebenen Maßen in dein Heft und beschrifte es wie in der Grafik. |
:Tipp {{versteckt| | :Tipp {{versteckt| | ||
| − | :Zeichne zunächst die Seite c, trage dann den Winkel <math>\alpha</math> an und | + | :Zeichne zunächst die Seite c, trage dann den Winkel <math>\alpha</math> an und anschließend die Seite b. }} |
*Übernimm auch die Eigenschaften eines Dreiecks. | *Übernimm auch die Eigenschaften eines Dreiecks. | ||
|} | |} | ||
| Zeile 34: | Zeile 38: | ||
| | | | ||
'''<span style="color:#ff0000">Eigenschaften des Dreiecks:</span>''' | '''<span style="color:#ff0000">Eigenschaften des Dreiecks:</span>''' | ||
| − | * | + | *Ein Dreieck wird durch '''drei Punkte A, B und C''' bestimmt, die nicht auf einer Geraden liegen. |
*Die '''Verbindungsstrecken''' zwischen den Punkten heißen '''Seiten'''. Seite '''a liegt dem Eckpunkt A''' gegenüber, Seite '''b dem Punkt B''', Seite '''c dem Punkt C.''' | *Die '''Verbindungsstrecken''' zwischen den Punkten heißen '''Seiten'''. Seite '''a liegt dem Eckpunkt A''' gegenüber, Seite '''b dem Punkt B''', Seite '''c dem Punkt C.''' | ||
| − | *Die '''Winkel''' werden '''<math>\alpha</math>, <math>\beta</math> und <math>\gamma</math>''' genannt. '''<math>\alpha</math> ist der Winkel | + | *Die '''Winkel''' werden '''<math>\alpha</math>, <math>\beta</math> und <math>\gamma</math>''' genannt. '''<math>\alpha</math> ist der Winkel beim Eckpunkt A''', '''<math>\beta</math> bei B''' und '''<math>\gamma</math> bei C.''' |
*Die Summe der Innenwinkel beträgt <math>\alpha</math> + <math>\beta</math> + <math>\gamma</math> = <math>180^\circ</math> | *Die Summe der Innenwinkel beträgt <math>\alpha</math> + <math>\beta</math> + <math>\gamma</math> = <math>180^\circ</math> | ||
|} | |} | ||
| Zeile 42: | Zeile 46: | ||
---- | ---- | ||
| − | <big>[[Lernpfad Flächenberechnung/Inhaltsverzeichnis/Dreieck/Flächenberechnung|Hier]]</big> | + | <big>[[Lernpfad Flächenberechnung/Inhaltsverzeichnis/Dreieck/Flächenberechnung|Hier]]</big> geht's weiter! |
Aktuelle Version vom 8. November 2010, 17:16 Uhr
Das Dreieck
|
Das Bermudadreieck ist die Bezeichnung für ein Seegebiet, das sich im westlichen Atlantik, nördlich der Karibik befindet. Schiffe verschwinden bei besten Wetterbedingungen und ruhiger See spurlos oder treiben als verlassene, aber völlig intakte Geisterschiffe im Meer, während die Mannschaften verschollen bleiben. Schiffskapitäne versuchen dieses Bermudadreieck möglichst nicht zu befahren. Wie groß ist nun die Fläche dieses "Dreiecks", das man besser meiden sollte? Bald wirst du sie selbst berechnen können. |
Das Dreieck
| 200px | Arbeitsauftrag:
|
Hier geht's weiter!
 an und anschließend die Seite b.
an und anschließend die Seite b. 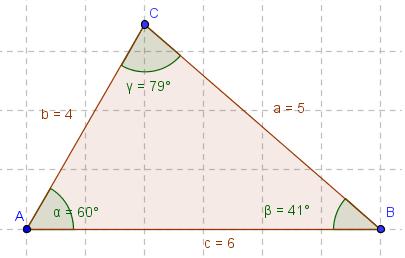
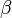 und
und 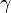 genannt.
genannt.