2003 II: Unterschied zwischen den Versionen
| (18 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:|Lösung gesamt]]</center> | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6 '''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:Andre Etzel_Abi_03_II_Lösungen1.doc|Lösung gesamt]]</center> |
| Zeile 24: | Zeile 24: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| + | '''Aufgabe 1'''<br /> | ||
| + | Gegeben ist die Schar der in IR definierten Funktionen | ||
| + | <math>f_k(x)=\frac{1}{2}\cdot(k-x)\cdot \sqrt{e^{x}}</math> mit <math>k \in \mathbb R</math> . Der jeweilige Graph von <math>f_k\,</math> wird mit | ||
| + | <math>G_k\,</math> bezeichnet.<br /> | ||
| − | </ | + | a) Geben Sie <math>f_k(0)\,</math> sowie die Nullstelle von <math>f_k\,</math> an. |
| + | Untersuchen Sie das Verhalten von <math> f_k\,</math> für <math>x\rightarrow -\infty</math> und für <math>x\rightarrow +\infty</math> | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Andre Etzel_Abi_03_II_1a.jpg|500px]] | ||
| − | + | }} | |
| − | < | + | b) Zeigen Sie, dass <math>f^{'}_k(x)= \frac{1}{2}f_{k-2}(x)</math> |
| + | gilt, und ermitteln Sie hiermit | ||
| + | Funktionsterme der Ableitungen <math>f^{''}_k\,</math> und <math>f^{'''}_k\,</math> sowie einer Stammfunktion | ||
| + | von <math>f_k\,</math> . | ||
| − | + | :{{Lösung versteckt| | |
| − | + | ||
| + | [[Bild:Andre Etzel_Abi_03_II_1b.jpg|500px]] | ||
| + | }} | ||
| − | + | c) Zeigen Sie, dass <math>G_k\,</math> genau einen Hochpunkt und genau einen Wendepunkt | |
| − | + | besitzt, und bestimmen Sie die Koordinaten dieser Punkte. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild]] | + | [[Bild:Andre Etzel_Abi_03_II_1c.jpg|500px]] |
}} | }} | ||
| − | |||
| + | d) Zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse <math>G_4\,</math> | ||
| + | und <math>G_6\,</math> in ein gemeinsames Koordinatensystem ein. | ||
| − | + | :{{Lösung versteckt| | |
| + | <ggb_applet width="795" height="512" version="3.2" ggbBase64="UEsDBBQACAAIALhekjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5VbNjts2ED43T0HwtAmwtkRJKxmwNmhTtAiQNAe3OeSQgpZGMmtZFEhqV87L9GH6Yh2Skv92myBBghx62JU0M5z55psfevl82DXkDpQWss1pOAsogbaQpWjrnPamus7o89snyxpkDWvFSSXVjpucRjNGrbwXt09+WOqNvCe8cSZvBdzntOKNBkp0p4CXegNgzuS8H0QjuNq/Wf8FhdFHhXfysu16jGJUj7JiV74Sevqcu4BdI8zP4k6UoEgji5zeJAgd396CMqLgTU7jwEtYTtmFEkWR1W6kEh9ka6z50XmFEkK0+ADICLOy5dwluoS+aEQpeGuTcTjQiJB7UZpNTtNFgi5B1BvEmoSB91ZIqcrVXhvYkeEdKInI4mwWhzGLWXoThxELYkr2oyqIZ1G2SFiWBRFLM+tSI2KEksSzYMHiNMjwEEtYiqr9pItmYRakSRLg4XTBUh8b7lZgDNZSEz6AngitlShP31/qn2RTHmrQSdGaF7wzvXJtEI2ildnbWMibsjn+2NYNjDKGVdpAsV3LYeV5i7zr3/edO+LgrOsXspGKKFsRRF+Pz7V/OhuL82AVOJvAWYw+rNODPlwwZ+Gea/90Vo1oPbQx73BKOpiiCE38N7HNO7HR8DVgL1DSt8K8mj6wZ7ZjoqG3/63frXFoTrvm4DL8Si6X84t2W25BtdD4pmqxrL3sNbmzzesr53CUUIgdfnrFyAe3tfoDAXhpCbWCCbefOM+W05417oV4OZ9AWAwasRYGVwfmY2wudrINTlVOV0bxf/7GadjhhP6C9cI0KCm5sVZ2lBrYAc6ZcQ3S9mgmigNbW2oRYNh+DI69P06+XTXSbY1Dw46HjrVA/X/0EC6YbsPxbRaOncL3CPA0b+fttSzHyOHEILLqUsVJ7rwDXG8AvuJm7HPSoUM3NYeSYB19rp/MWl9mffN/yBous2azNMxYZv/iZBHEyffloBIDlF5yMu3TBXauOMt6wMtP24t1glnh5Togi9XV8JTkBG9bMicM/z8jV1tyTVD6jMD7q8GLn1Iyf8Be1bdu4ujR6fnCMxtcLS0GxqE5Vughg2fb6XECpyWdhA84DD7K4Zuq0mDIgHcHHt3n9DqKH6U4ulzXH0Ff4I1kyXQHf/0z/jTf9ch3/Qjf+kv5rr8d35bnQ8c68j+b75R9K75vLvmen14A7jfS+CPx9l9QSwcIWOlgv4ADAABWCgAAUEsBAhQAFAAIAAgAuF6SPFjpYL+AAwAAVgoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAC6AwAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| − | |||
| + | e) <math>G_4\,</math> schließt im zweiten Quadranten mit den Koordinatenachsen ein | ||
| + | sich ins Unendliche erstreckendes Flächenstück ein. Begründen Sie, | ||
| + | dass dieses einen endlichen Inhalt hat. | ||
| − | + | :{{Lösung versteckt| | |
| − | + | [[Bild:Andre Etzel_Abi_03_II_1e.jpg|500px]] | |
| − | + | ||
| − | [[Bild:]] | + | |
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | f) Geben Sie an, welche Bedeutung die Funktion <math>2 \cdot f_6\,</math> für die Funktion | ||
| + | <math>f_4\,</math> hat. Bestimmen Sie mit Hilfe von <math>G_6\,</math> aus Ihrer Zeichnung die positive | ||
| + | Zahl z (auf eine Dezimale genau), für die <math>\int_{0}^{z} f_4 (x)\,dx =0</math> | ||
| + | ist. | ||
| + | Tragen Sie dazu entsprechende Hilfslinien in die Zeichnung ein und | ||
| + | erläutern Sie Ihr Vorgehen. | ||
| + | Überprüfen Sie Ihre graphisch gewonnene Näherungslösung, indem | ||
| + | Sie z mit Hilfe des Taschenrechners auf eine Dezimale genau ermitteln. | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:]] | + | [[Bild:Andre Etzel_Abi_03_II_1f.jpg|500px]] |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 118: | Zeile 102: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | + | '''Aufgabe 2'''<br /> | |
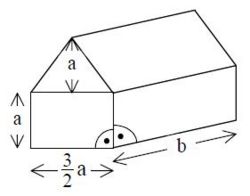
| − | Das | + | Das abgebildete Zelt [[Bild:Straßheimer_Florian_Graph_abiaufgabe_03.jpg |250px| right]] - geometrisch betrachtet |
| + | ein gerades Prisma - hat einen rechteckigen | ||
| + | Grundriss mit den Seitenlängen <math>\frac{3}{2}a</math> | ||
| + | und <math>b\,</math> | ||
| + | . Die Front besteht aus einem Rechteck mit | ||
| + | den Seitenlängen <math>\frac{3}{2}a</math> und <math>a\,</math> sowie einem | ||
| + | aufgesetzten gleichschenkligen Dreieck der | ||
| + | Höhe <math>a\,</math>. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | a) Zeigen Sie, dass für den Rauminhalt V des Zelts und für den Flächeninhalt | ||
| + | S der benötigten Zeltplane (ohne Boden und Laschen, das | ||
| + | Zelt ist vollständig geschlossen) gilt: | ||
| − | + | <math>V=\frac{9}{4}a^{2}b</math> | |
| − | + | <math>S=\frac{9}{2}a^{2}+ \frac{9}{2}ab</math>. | |
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Andre Etzel_Abi_03_II_2a.jpg|500px]] | ||
| − | + | }} | |
| + | b) Bestimmen Sie a und b so, dass <math>V = 121,5 m^{3}\,</math> ist und dass der Materialverbrauch | ||
| + | an Zeltplane möglichst gering ist. Wie viele <math>m^{2}\,</math> Zeltplane | ||
| + | werden in diesem Fall benötigt? | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | |||
| − | |||
| − | + | [[Bild:Andre Etzel_Abi_03_II_2b.jpg|500px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [[Bild:]] | + | |
}} | }} | ||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 18. April 2010, 11:10 Uhr
|
|
|
Aufgabe 1 Gegeben ist die Schar der in IR definierten Funktionen
a) Geben Sie b) Zeigen Sie, dass c) Zeigen Sie, dass
|
|
Aufgabe 2 ein gerades Prisma - hat einen rechteckigen
Grundriss mit den Seitenlängen
b) Bestimmen Sie a und b so, dass
|
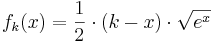 mit
mit 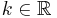 . Der jeweilige Graph von
. Der jeweilige Graph von 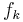 wird mit
wird mit
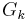 bezeichnet.
bezeichnet.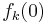 sowie die Nullstelle von
sowie die Nullstelle von 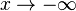 und für
und für 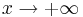

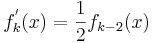 gilt, und ermitteln Sie hiermit
Funktionsterme der Ableitungen
gilt, und ermitteln Sie hiermit
Funktionsterme der Ableitungen 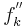 und
und 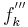 sowie einer Stammfunktion
von
sowie einer Stammfunktion
von 

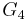 und
und 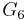 in ein gemeinsames Koordinatensystem ein.
in ein gemeinsames Koordinatensystem ein.

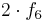 für die Funktion
für die Funktion
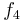 hat. Bestimmen Sie mit Hilfe von
hat. Bestimmen Sie mit Hilfe von 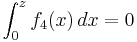 ist.
Tragen Sie dazu entsprechende Hilfslinien in die Zeichnung ein und
erläutern Sie Ihr Vorgehen.
Überprüfen Sie Ihre graphisch gewonnene Näherungslösung, indem
Sie z mit Hilfe des Taschenrechners auf eine Dezimale genau ermitteln.
ist.
Tragen Sie dazu entsprechende Hilfslinien in die Zeichnung ein und
erläutern Sie Ihr Vorgehen.
Überprüfen Sie Ihre graphisch gewonnene Näherungslösung, indem
Sie z mit Hilfe des Taschenrechners auf eine Dezimale genau ermitteln.

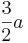 und
und 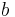 . Die Front besteht aus einem Rechteck mit
den Seitenlängen
. Die Front besteht aus einem Rechteck mit
den Seitenlängen 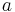 sowie einem
aufgesetzten gleichschenkligen Dreieck der
Höhe
sowie einem
aufgesetzten gleichschenkligen Dreieck der
Höhe 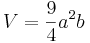
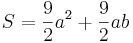 .
.

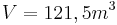 ist und dass der Materialverbrauch
an Zeltplane möglichst gering ist. Wie viele
ist und dass der Materialverbrauch
an Zeltplane möglichst gering ist. Wie viele 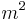 Zeltplane
werden in diesem Fall benötigt?
Zeltplane
werden in diesem Fall benötigt?


