2003 I: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6'''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] </center> | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=56690cea22e20298b306940dfaa656c6'''Download der Originalaufgaben: Abitur 2003 LK Mathematik Bayern'''] - [[Media:Abi_2003_I_Lösung.pdf|Lösung gesamt]] </center> |
| Zeile 30: | Zeile 30: | ||
; Zeichnen Sie mit Hilfe der Funktionswerte g(-1) , g(1) und g(2) den Graphen von g im Bereich -2<math>\le</math>x<math>\le</math>2 in ein Koordinatensystem mit der Längeneinheit 2 cm. <br /> | ; Zeichnen Sie mit Hilfe der Funktionswerte g(-1) , g(1) und g(2) den Graphen von g im Bereich -2<math>\le</math>x<math>\le</math>2 in ein Koordinatensystem mit der Längeneinheit 2 cm. <br /> | ||
; Erläutern Sie, wie der Graph von g<sup>*</sup> aus dem Graphen von g und schließlich der Graph von f<sub>1</sub> aus den Graphen von g und g<sup>*</sup> entsteht. Zeichnen Sie die Graphen von g<sup>*</sup> und f<sub>1</sub> in das vorhandene Koordinatensystem. <div align="right">''6 BE''</div> | ; Erläutern Sie, wie der Graph von g<sup>*</sup> aus dem Graphen von g und schließlich der Graph von f<sub>1</sub> aus den Graphen von g und g<sup>*</sup> entsteht. Zeichnen Sie die Graphen von g<sup>*</sup> und f<sub>1</sub> in das vorhandene Koordinatensystem. <div align="right">''6 BE''</div> | ||
| + | <br /> | ||
| − | + | '''Hinweis:''' Die Entstehung von Graphen aus anderen Graphen kann in [[Facharbeit Florian Wilk/Strecken und Spiegeln von Funktionsgraphen|diesem Lernpfad]] wiederholt werden. | |
| + | <br /> <br /> <br /> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | [[Bild:Abi_2003_I_Lösung_1a.png|700px]] | |
}} | }} | ||
| Zeile 49: | Zeile 51: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | [[Bild:Abi_2003_I_Lösung_1b.png|700px]] | |
}} | }} | ||
| Zeile 58: | Zeile 60: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | [[Bild:Abi_2003_I_Lösung_1c.png|700px]] | |
}} | }} | ||
| Zeile 69: | Zeile 71: | ||
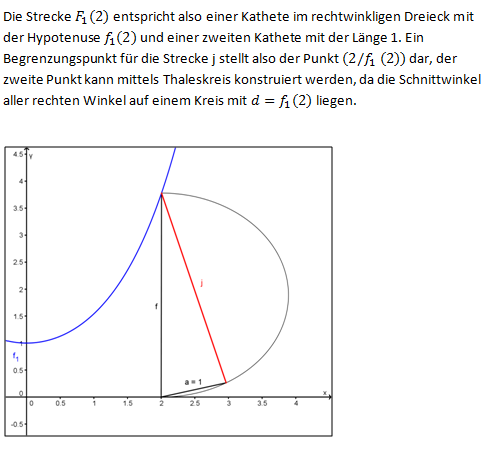
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | [[Bild:Abi_2003_I_Lösung_1d_1.png|700px]] | |
| + | [[Bild:Abi_2003_I_Lösung_1d_2.png|700px]] | ||
}} | }} | ||
| Zeile 90: | Zeile 93: | ||
| − | |||
| − | |||
| − | |||
| + | <popup name="Tipp"> | ||
| + | [[Bild:Abi_2003_I_2a_Tipp.png|700px]] | ||
| + | </popup> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Abi_2003_I_Lösung_2a.png|700px]] | ||
| + | [[Bild:Abi_2003_I_2a_Zusatz.png|700px]] | ||
| + | }} | ||
;b) Lässt man das im 1. Quadranten liegende, von G<sub>1</sub>, der positiven y-Achse und der Geraden mit der Gleichung y = 10 begrenzte Flächenstück um die y-Achse rotieren, entsteht ein kelchförmiger Körper. Berechnen Sie dessen Durchmesser d am oberen Rand. | ;b) Lässt man das im 1. Quadranten liegende, von G<sub>1</sub>, der positiven y-Achse und der Geraden mit der Gleichung y = 10 begrenzte Flächenstück um die y-Achse rotieren, entsteht ein kelchförmiger Körper. Berechnen Sie dessen Durchmesser d am oberen Rand. | ||
; Geben Sie einen Ansatz für das Volumen V des Kelches an (Berechnung ist nicht verlangt). <div align="right">''5 BE''</div> | ; Geben Sie einen Ansatz für das Volumen V des Kelches an (Berechnung ist nicht verlangt). <div align="right">''5 BE''</div> | ||
| + | |||
| + | <popup name="Tipp"> | ||
| + | [[Bild:Abi_2003_I_2b_Tipp.png|700px]] | ||
| + | </popup> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | [[Bild:Abi_2003_I_Lösung_2b.png|700px]] | |
}} | }} | ||
| Zeile 119: | Zeile 131: | ||
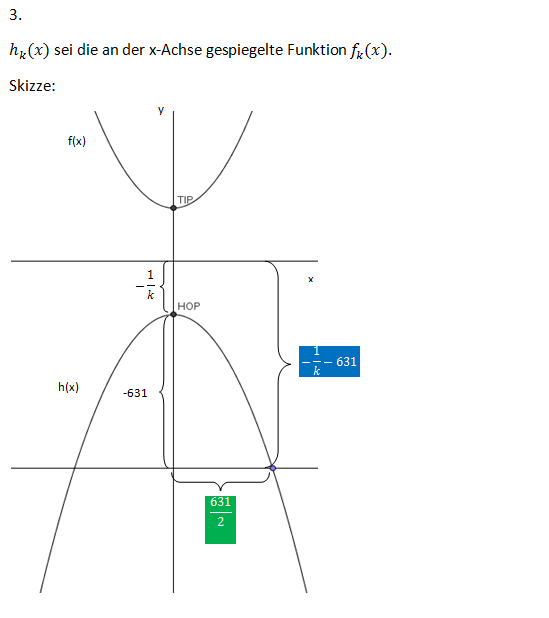
; Die Spannweite am Boden (Außenmaße)und die Höhe des 1965 in St. Louis, Missouri, errichteten Gateway Arch betragen jeweils 631 feet. Das Foto zeigt eine Schrägansicht des Bogens. In einem Koordinatensystem mit der Längeneinheit 1 foot kann die äußere Begrenzung des Bogens durch einen umgedrehten Graphen G<sub>k</sub> angenähert werden. Erstellen Sie einen Ansatz zur Berechnung von k und zeigen Sie, dass der Wert k=2<sup>-7</sup> eine gute Näherungslösung ist. <div align="right">''6 BE''</div> | ; Die Spannweite am Boden (Außenmaße)und die Höhe des 1965 in St. Louis, Missouri, errichteten Gateway Arch betragen jeweils 631 feet. Das Foto zeigt eine Schrägansicht des Bogens. In einem Koordinatensystem mit der Längeneinheit 1 foot kann die äußere Begrenzung des Bogens durch einen umgedrehten Graphen G<sub>k</sub> angenähert werden. Erstellen Sie einen Ansatz zur Berechnung von k und zeigen Sie, dass der Wert k=2<sup>-7</sup> eine gute Näherungslösung ist. <div align="right">''6 BE''</div> | ||
| − | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | [[Bild:Abi_2003_I_3_Skizze.png|700px]] | |
| + | [[Bild:Abi_2003_I_Lösung_3.png|700px]] | ||
}} | }} | ||
| + | |||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 11. April 2010, 16:57 Uhr
|
|
g: x →
Hinweis: Die Entstehung von Graphen aus anderen Graphen kann in diesem Lernpfad wiederholt werden.
|
[Ergebnis:
|
|
 definierten Funktionen
definierten Funktionen 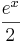 , g*:x →
, g*:x → 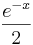 und f1: x →
und f1: x → 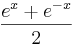 .
.
 x
x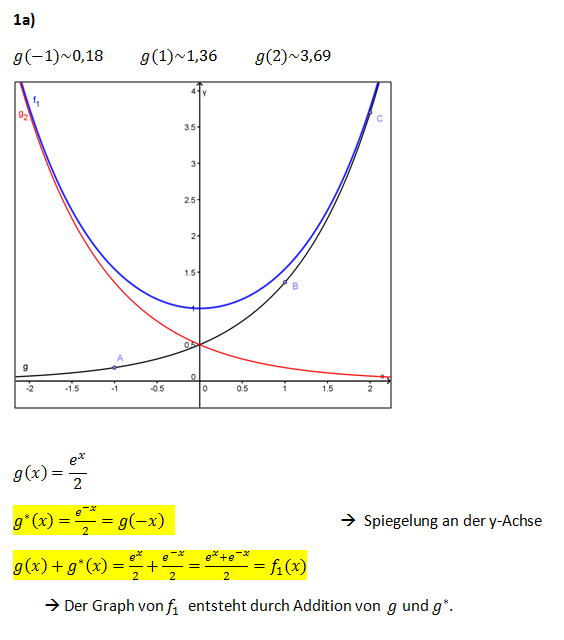
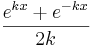 mit D =
mit D = 

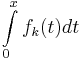 mit dem Definitionsbereich
mit dem Definitionsbereich 
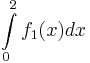 als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig.
als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig. 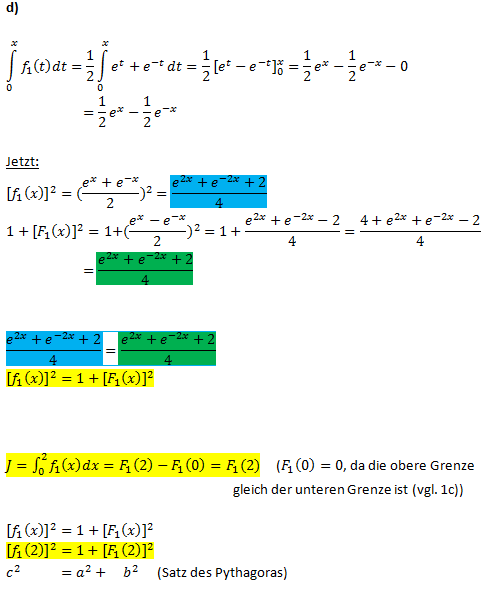
 ]
]