2004 VI: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
K |
K (Angabe in eigenen Kasten gesetzt) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 26: | Zeile 26: | ||
In einem kartesischen Koordinatensystem des '''R'''<sup>3</sup> sind die Punkte <math>O \left( 0 / 0 / 0 \right)</math>, <math>A \left( 10 / 0 / 0 \right)</math>, <math>B \left( 0 / 4 / 0 \right)</math>, <math>S \left( 0 / 0 / 6 \right)</math> sowie die Ebenenschar E<sub>t</sub>: 3x<sub>2</sub> + tx<sub>3</sub> - 3t = 0 mit t <math>\in</math> '''R''' gegeben. Die Punkte A, B und S legen die Ebene F fest. | In einem kartesischen Koordinatensystem des '''R'''<sup>3</sup> sind die Punkte <math>O \left( 0 / 0 / 0 \right)</math>, <math>A \left( 10 / 0 / 0 \right)</math>, <math>B \left( 0 / 4 / 0 \right)</math>, <math>S \left( 0 / 0 / 6 \right)</math> sowie die Ebenenschar E<sub>t</sub>: 3x<sub>2</sub> + tx<sub>3</sub> - 3t = 0 mit t <math>\in</math> '''R''' gegeben. Die Punkte A, B und S legen die Ebene F fest. | ||
| + | </td></tr></table></center> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| Zeile 104: | Zeile 111: | ||
:'''b)''' Die Ebenenschar E<sub>t</sub> enthält neben der x<sub>1</sub>x<sub>3</sub> - Ebene eine weitere Tangentialebene von K. Berechnen Sie den zugehörigen Wert von t. <div align="right">''7 BE''</div> | :'''b)''' Die Ebenenschar E<sub>t</sub> enthält neben der x<sub>1</sub>x<sub>3</sub> - Ebene eine weitere Tangentialebene von K. Berechnen Sie den zugehörigen Wert von t. <div align="right">''7 BE''</div> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:Abitur 2004 VI Aufg | + | [[Bild:Abitur 2004 VI Aufg 3b.jpg|750px]] |
}} | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 7. April 2010, 14:38 Uhr
|
|
|
In einem kartesischen Koordinatensystem des R3 sind die Punkte |
|
Die Punkte A, B, O und S bilden die Ecken der Pyramide ABOS.
(Hinweis: Zerlegen Sie einen der beiden Teilkörper in ein dreiseitiges Prisma und eine dreiseitige Pyramide.) |
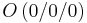 ,
, 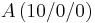 ,
, 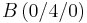 ,
, 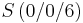 sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t
sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t  R gegeben. Die Punkte A, B und S legen die Ebene F fest.
R gegeben. Die Punkte A, B und S legen die Ebene F fest.


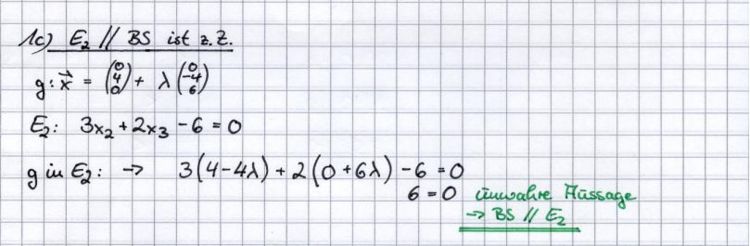

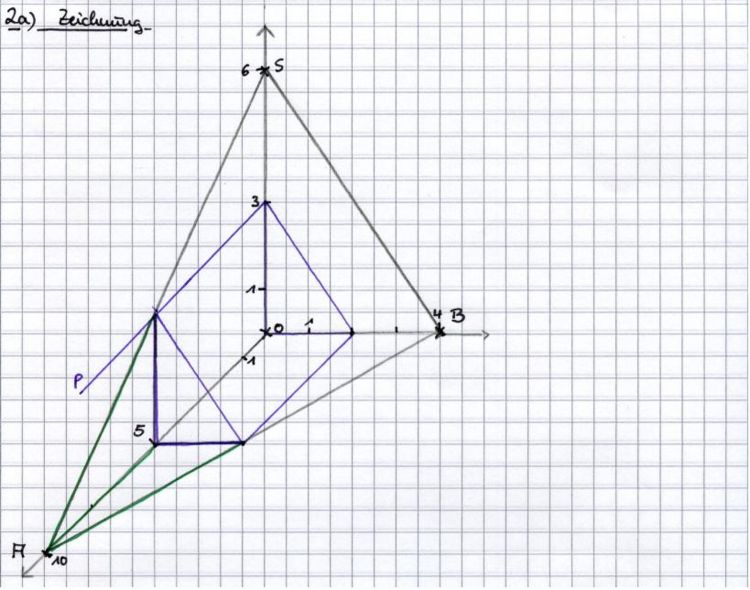


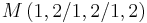 der Mittelpunkt der Inkugel K der Pyramide ABOS ist.
der Mittelpunkt der Inkugel K der Pyramide ABOS ist. 


