2005 VI: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 46: | Zeile 46: | ||
;Bemerkung | ;Bemerkung | ||
| − | Eine andere | + | Eine andere Möglichkeit wäre, mit Hilfe des Vektorprodukts den Normalenvektor der Ebene aufzustellen. |
{{Lösung versteckt| | {{Lösung versteckt| | ||
| Zeile 69: | Zeile 69: | ||
.[[Bild:Abi 2005 VI 1c.jpg]]}} | .[[Bild:Abi 2005 VI 1c.jpg]]}} | ||
| − | + | ;Bemerkung | |
| + | Dass die beiden Richtungsvektoren linear abhängig sind, hat zur Folge, dass die die beiden Geraden echt parallel oder identisch sind. Man muss erst noch beweisen, dass sie nicht identisch sind, indem man beispielsweise überprüft, ob der Punkt A auf der Geraden g liegt. Das ist nicht der Fall. Daraus folgt, dass die beiden Geraden echt parallel sind. | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 142: | Zeile 143: | ||
}} | }} | ||
| + | ;Bemerkung | ||
| + | Die Projektion von M in die x<sub>3</sub>-Ebene heißt, dass die x<sub>1</sub>- und x<sub>2</sub>-Werte erhalten bleiben und der x<sub>3</sub>-Wert in diesem Fall 3 ist. | ||
| + | |||
| + | |||
| + | |||
| + | |||
c) Die Kugel wird nun angestoßen und rollt auf die Ebene E zu. Geben Sie eine Gleichung der Geraden m an, auf der sich dabei der Mittelpunkt der Kugel bewegt. | c) Die Kugel wird nun angestoßen und rollt auf die Ebene E zu. Geben Sie eine Gleichung der Geraden m an, auf der sich dabei der Mittelpunkt der Kugel bewegt. | ||
Begründen Sie, weshalb der Punkt, in dem die Kugel schließlich die Ebene E berührt, nicht mit dem Schnittpunkt von m und E zusammenfällt. | Begründen Sie, weshalb der Punkt, in dem die Kugel schließlich die Ebene E berührt, nicht mit dem Schnittpunkt von m und E zusammenfällt. | ||
| Zeile 152: | Zeile 159: | ||
}} | }} | ||
| − | + | ;Bemerkung | |
| + | Der Normalenvektor der Ebene und der Richtungsvektor von m sind nicht linear abhängig. Daraus folgt, dass m nicht senkrecht auf der Ebene steht. Der Berührpunkt einer Kugel mit eine Ebene liegt aber immer auf einer senkrechten Geraden zur Ebene durch den Mittelpunkt der Kugel. Somit ist der Berührpunkt nicht der Schnittpunkt der Geraden m mit der Ebene. | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 23. März 2010, 16:32 Uhr
|
|
|
In einem kartesischen Koordinatensystem ist die Geradenschar
ga : |
a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform. [mögliches Ergebnis E: x1 + 2x2 + 2x3 - 10 = 0] 3 BE
Eine andere Möglichkeit wäre, mit Hilfe des Vektorprodukts den Normalenvektor der Ebene aufzustellen.
b) Berechnen Sie den Schnittwinkel zwischen der Geraden g-1 und der Ebene E. 3 BE
4 BE
Dass die beiden Richtungsvektoren linear abhängig sind, hat zur Folge, dass die die beiden Geraden echt parallel oder identisch sind. Man muss erst noch beweisen, dass sie nicht identisch sind, indem man beispielsweise überprüft, ob der Punkt A auf der Geraden g liegt. Das ist nicht der Fall. Daraus folgt, dass die beiden Geraden echt parallel sind. |
a) Der Punkt C wird an der Geraden AB gespiegelt. Ermitteln Sie die Koordinaten des Spiegelpunkts C*. [Ergebnis: C* = (4/8/-5)] 5 BE
4 BE
6 BE
|
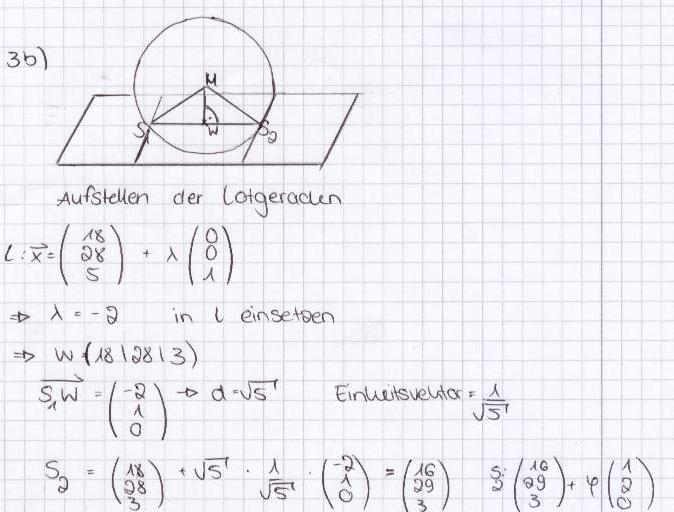
In der Ebene H: x3 = 3 liegen zwei parallele Schienen s1 und s2.Die Schiene s1 wird durch die Gerade s1 : a) Berechnen Sie die Koordinaten des Punkts S, in dem die Kugel die Schiene s1 berührt. [Ergebnis: S = (20/27/3)] 6 BE
5 BE
Die Projektion von M in die x3-Ebene heißt, dass die x1- und x2-Werte erhalten bleiben und der x3-Wert in diesem Fall 3 ist.
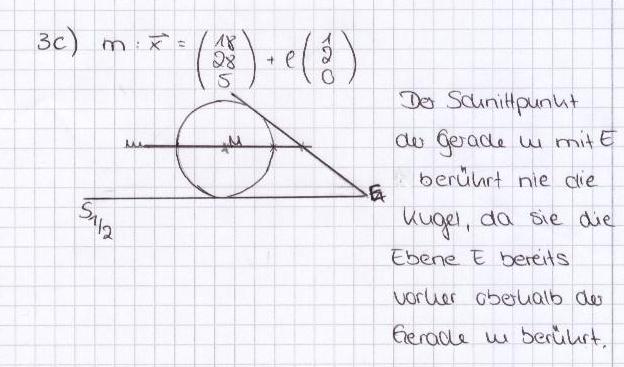
c) Die Kugel wird nun angestoßen und rollt auf die Ebene E zu. Geben Sie eine Gleichung der Geraden m an, auf der sich dabei der Mittelpunkt der Kugel bewegt. Begründen Sie, weshalb der Punkt, in dem die Kugel schließlich die Ebene E berührt, nicht mit dem Schnittpunkt von m und E zusammenfällt. 4 BE
Der Normalenvektor der Ebene und der Richtungsvektor von m sind nicht linear abhängig. Daraus folgt, dass m nicht senkrecht auf der Ebene steht. Der Berührpunkt einer Kugel mit eine Ebene liegt aber immer auf einer senkrechten Geraden zur Ebene durch den Mittelpunkt der Kugel. Somit ist der Berührpunkt nicht der Schnittpunkt der Geraden m mit der Ebene. |
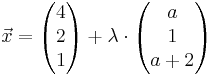 mit a,
mit a, 

 - gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird.
- gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird.

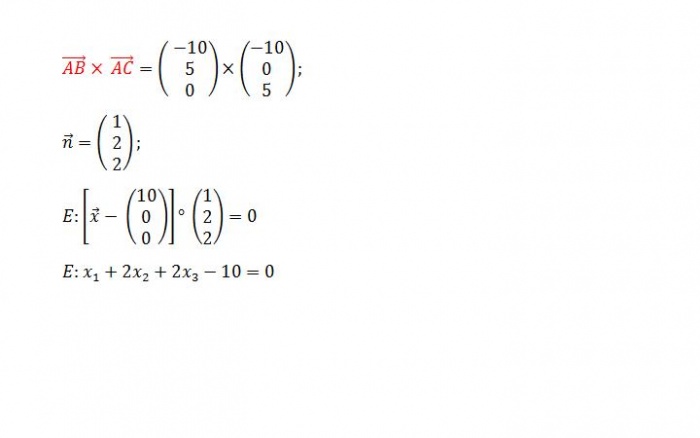



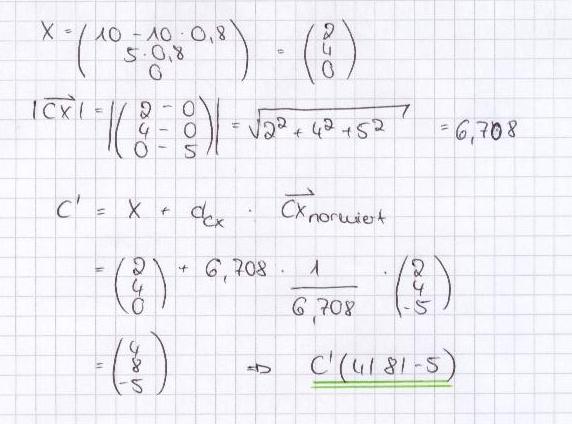
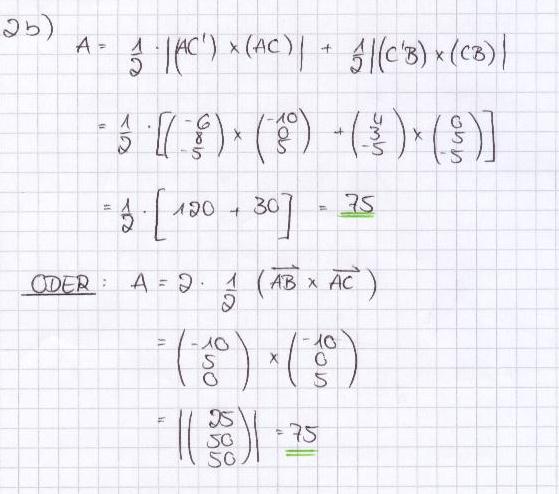

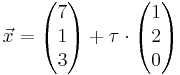 mit
mit