2007 II: Unterschied zwischen den Versionen
K |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 65: | Zeile 65: | ||
ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1. | ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1. | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt|1= |
| − | [[Bild:Infini07-1e.jpg|750px]] | + | [[Bild:Infini07-1e.jpg|750px]]<br /> |
| + | '''Erläuterung:'''<br /> | ||
| + | Sei <math>\frac{x}{x-1}</math> = <math>g(x)</math>;<br /> | ||
| + | D<sub>g</sub> = IR\{+1}<br /> | ||
| + | <math>\Rightarrow</math> deswegen muss hier <math>\lim_{a \to 1}</math> verwendet werden (''uneigentliches Integral'')! | ||
}} | }} | ||
Aktuelle Version vom 27. Februar 2010, 16:48 Uhr
|
|
1. Gegeben ist die Funktion
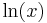 strebt hier, analog zu strebt hier, analog zu 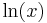 beim Grenzwert für x beim Grenzwert für x 1-, genau genommen gegen 0+ statt gegen 0. Ist aber für das Ergebnis egal (+ 1-, genau genommen gegen 0+ statt gegen 0. Ist aber für das Ergebnis egal (+ ). ).
|
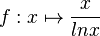 mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
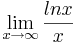 = 0 darf ohne Beweis verwendet werden.)
= 0 darf ohne Beweis verwendet werden.)

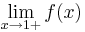 :
: 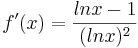 ]
]


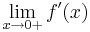 und skizzieren Sie Gf unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem.
und skizzieren Sie Gf unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem.
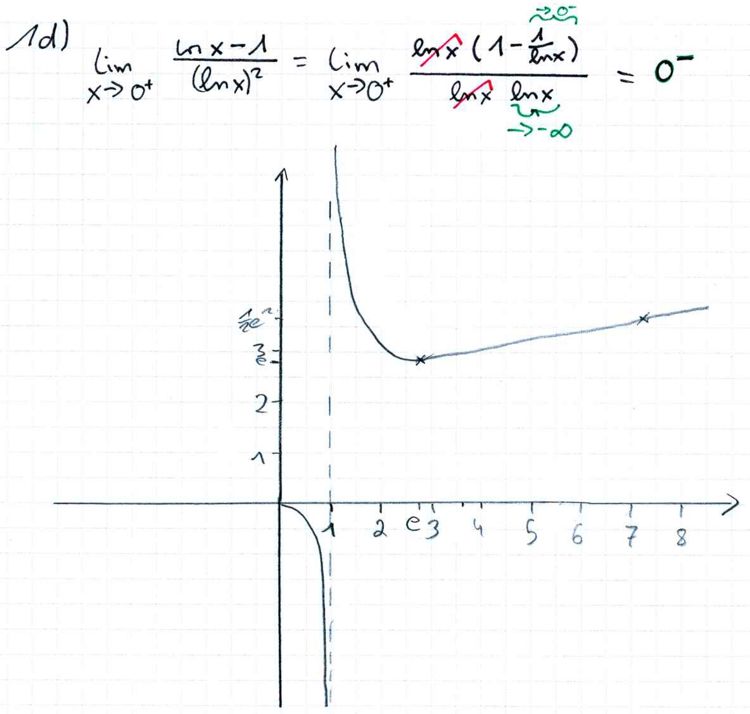
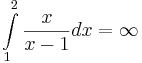 .
Was folgt für
.
Was folgt für 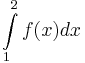 ? Begründen Sie Ihre Antwort. Dabei dürfen Sie
ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1.
? Begründen Sie Ihre Antwort. Dabei dürfen Sie
ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1.
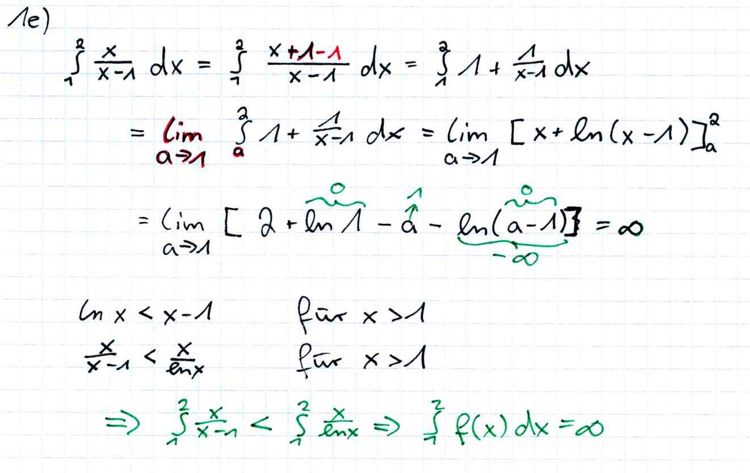
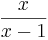 =
= 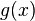 ;
; deswegen muss hier
deswegen muss hier 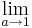 verwendet werden (uneigentliches Integral)!
verwendet werden (uneigentliches Integral)!
 besitzt.
besitzt.



