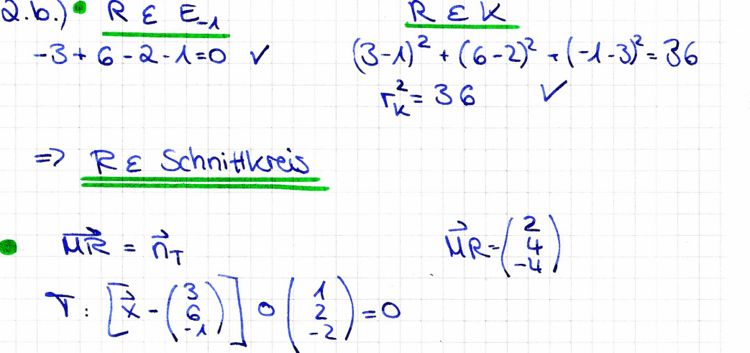2007 V: Unterschied zwischen den Versionen
(Abituraufgabe_2007_Anfang) |
|||
| (15 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | __NOTOC__ | + | {| class="wikitable " |
| + | |- style="background: #DDFFDD;" | ||
| + | |} | ||
| + | [[Kategorie:Name der Kategorie]]__NOTOC__ | ||
| + | |||
<div style="padding:1px;background: #EEEEE6;border:0px groove;"> | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| − | + | <br /> | |
| − | + | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| Zeile 8: | Zeile 11: | ||
<center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2007'''</big></center> | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2007'''</big></center> | ||
<center><big>'''Analytische Geometrie V'''</big></center> | <center><big>'''Analytische Geometrie V'''</big></center> | ||
| + | <br /> | ||
| + | <center>'''Lösung von Ruth Burkard, Julian Weinbeer und Veronika Weinbeer'''</center> | ||
| + | <br> | ||
| + | [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=2ad4ccef77e003c1a9ba1d85ca3ba82a Angabe] <br /> | ||
| + | [[Media:Abi_2007_V_gesamte_Loesung.doc|gesamte Lösung]] | ||
| + | </td></tr></table></center> | ||
| − | |||
| − | |||
</div> | </div> | ||
| − | |||
<div style="padding:1px;background: #EEEEE6;border:0px groove;"> | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| − | |||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | + | <div style="margin:0px; margin-right:90px; border: solid thin black; padding: 1em 1em 1em 1em; background-color:white; width:97%; align:center; "> | |
| + | <div align="left"> | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | Gegeben ist in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Ebenenschar E<sub>k</sub> : | + | Gegeben ist in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Ebenenschar E<sub>k</sub> : kx<sub>1</sub> + k <sup>2</sup>x<sub>2</sub> + 2x<sub>3</sub>- k<sup>2</sup> = 0 , mit k ∈ IR als Scharparameter. |
<br><br> | <br><br> | ||
| − | |||
| + | '''a)''' Ermitteln Sie, für welche Werte von k die Ebene E<sub>k</sub> den Punkt P(1|2|-3)und zugleich den Punkt Q(0|1|0) enthält. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild:Aufgabe_1_a.jpg| | + | [[Bild:Aufgabe_1_a.jpg|750px]] |
}} | }} | ||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | <br> | ||
| + | |||
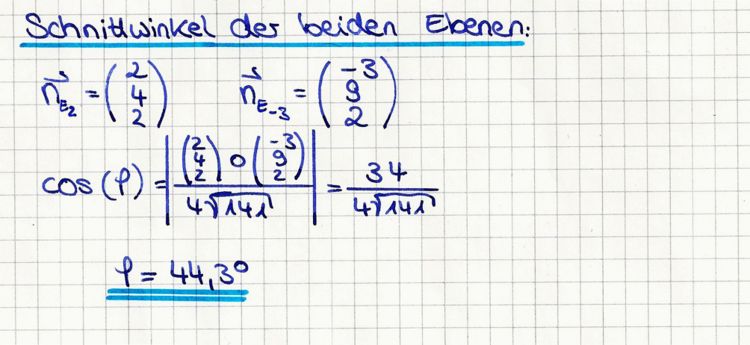
| + | '''b)''' Die beiden Ebenen E<sub>2</sub> und E<sub>-3</sub> schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und | ||
| + | :den Schnittwinkel der beiden Ebenen auf eine Dezimale gerundet. | ||
| + | |||
| + | [mögliches Teilergebnis: g: <math>\vec x = \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 1 \\ 1 \\ -3 \end{pmatrix}</math>, λ ∈ IR ] | ||
| + | <br><br> | ||
| + | |||
| + | :;Bestimmung der Gleichung in Parameterform: | ||
| + | |||
| + | :1. Lösungsweg: | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_b_Loesung_I.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | :2. Lösungsweg: | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_b_Loesung_II.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | :3. Lösungsweg: aus a) weiß man, dass P und Q auf allen Ebenen liegen; deshalb einen Punkt als Orstvektor nehmen und aus beiden Punkten den Richtungsvektor bestimmen (schnellster Lösungsweg) | ||
| + | <br> | ||
| + | |||
| + | :;Berechnung des Schnittwinkels: | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_b_Loesung_Winkel.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | |||
| + | |||
| + | '''c)''' Mit e(k) werde der Betrag des Abstands der Ebene E<sub>k</sub> vom Koordinatenursprung bezeichnet. Zeigen Sie, dass e(k)=<math>\frac{k^2}{\sqrt{k^2+k^4+2}} </math> und dass e(k)<1 ist. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_c.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | |||
| + | <br /> | ||
| + | '''d)''' Es gibt zwei Scharebenen, deren Schnittwinkel mit der x<sub>3</sub>-Achse 30° besteht. Ermitteln Sie die zugehörigen Werte von k. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_d.jpg|750px]] | ||
| + | }} | ||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | |||
| + | '''e)''' Untersuchen Sie, ob die Gerade g aus Teilaufgabe 1b senkrecht auf einer Ebene der Schar E<sub>k</sub> steht. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_e.jpg|750px]] | ||
| + | }} | ||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | '''Aufgabe 2:''' | ||
| + | |||
| + | Nun ist weiter die Kugel K mit dem Mittelpunkt M(1|2|3) und dem Radius r= 6 gegeben. Die Scharebene E<sub>-1</sub> schneidet die Kugel K in einem Kreis k<sub>s</sub> mit dem Mittelpunkt N und dem Radius r<sub>s</sub>. | ||
| + | |||
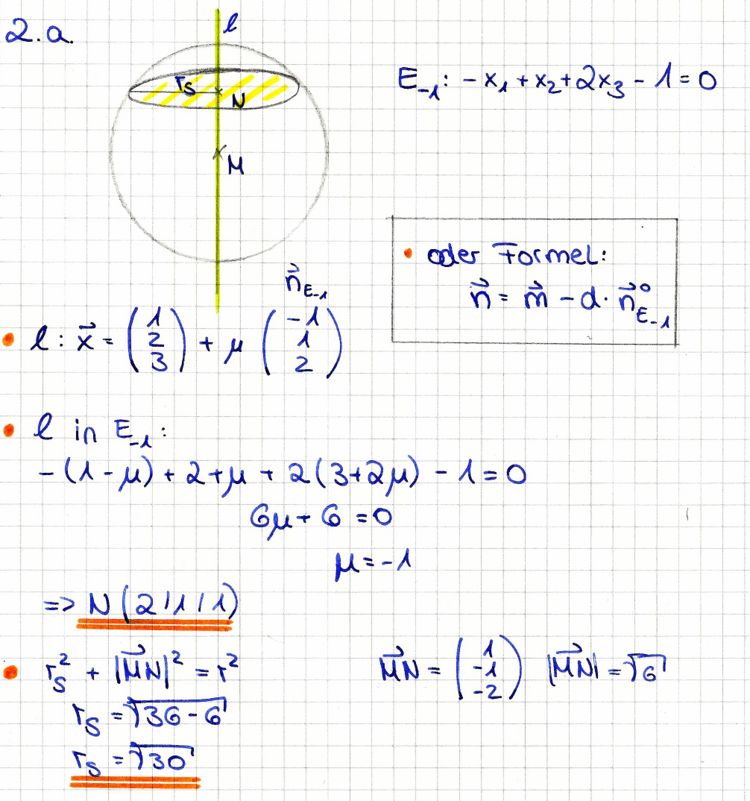
| + | '''a)''' Berechnen Sie die Koordinaten N und den Radius r<sub>s</sub> | ||
| + | :[Ergebnis: N(2|1|1); r<sub>s</sub> =<math>{\sqrt{30}}</math>] | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_2_a.jpg|750px]] | ||
| + | }} | ||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | |||
| + | '''b)''' Zeigen Sie, dass der Punkt R(3|6|-1) auf dem Schnittkreis k<sub>s</sub> liegt, und stellen Sie eine Gleichung der Tangentialebene T | ||
| + | :auf, die die Kugel K im Punkt R berührt. | ||
| + | :[mögliches Teilergebnis: T:x<sub>1</sub>+2x<sub>2</sub>-2x<sub>3</sub>-17=0] | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_2_b.jpg|750px]] | ||
| + | }} | ||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | |||
| + | '''c)''' Die Ebene E<sub>-1</sub> und die Tangentialebene an die Kugel K in allen Punkten des Schnittkreises k<sub>s</sub> begrenzen einen geraden | ||
| + | :Kreiskegel. Berechnen Sie das Volumen dieses Kegels. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_2_c.jpg|750px]] | ||
| + | }} | ||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | |||
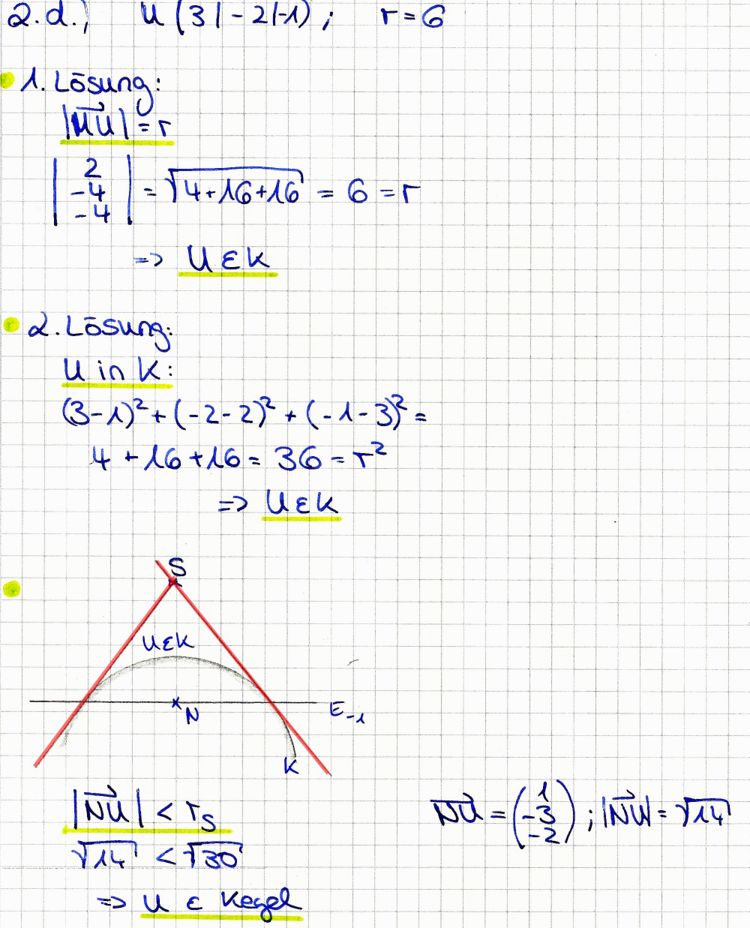
| + | '''d)''' Zeigen Sie, dass der Punkt U(3|-2|-1) auf der Kugel K und innerhalb des Kreiskegels liegt. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_2_d.jpg|750px]] | ||
| + | }} | ||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | |||
| + | </div> | ||
Aktuelle Version vom 3. März 2010, 16:27 Uhr
|
|
Gegeben ist in einem kartesischen Koordinatensystem des IR3 die Ebenenschar Ek : kx1 + k 2x2 + 2x3- k2 = 0 , mit k ∈ IR als Scharparameter.
a) Ermitteln Sie, für welche Werte von k die Ebene Ek den Punkt P(1|2|-3)und zugleich den Punkt Q(0|1|0) enthält. 4 BE
b) Die beiden Ebenen E2 und E-3 schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und
[mögliches Teilergebnis: g:
5 BE
4 BE
5 BE
e) Untersuchen Sie, ob die Gerade g aus Teilaufgabe 1b senkrecht auf einer Ebene der Schar Ek steht. 3 BE
Nun ist weiter die Kugel K mit dem Mittelpunkt M(1|2|3) und dem Radius r= 6 gegeben. Die Scharebene E-1 schneidet die Kugel K in einem Kreis ks mit dem Mittelpunkt N und dem Radius rs. a) Berechnen Sie die Koordinaten N und den Radius rs
6 BE
b) Zeigen Sie, dass der Punkt R(3|6|-1) auf dem Schnittkreis ks liegt, und stellen Sie eine Gleichung der Tangentialebene T
4 BE
c) Die Ebene E-1 und die Tangentialebene an die Kugel K in allen Punkten des Schnittkreises ks begrenzen einen geraden
5 BE
d) Zeigen Sie, dass der Punkt U(3|-2|-1) auf der Kugel K und innerhalb des Kreiskegels liegt. 4 BE
|

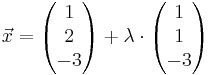 , λ ∈ IR ]
, λ ∈ IR ]


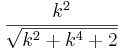 und dass e(k)<1 ist.
und dass e(k)<1 ist.


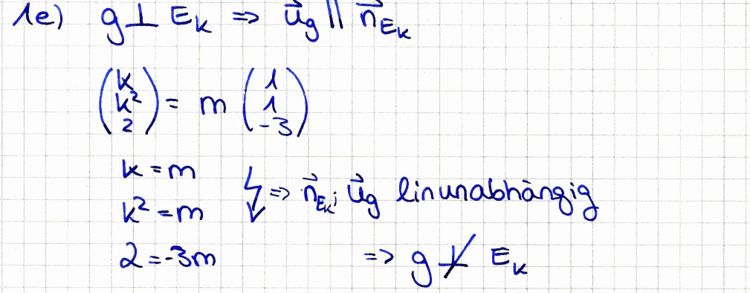
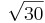 ]
]