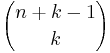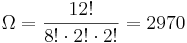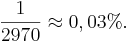2007 IV: Unterschied zwischen den Versionen
K |
K (Bemerkung zu Aufgabe 3b) |
||
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
| − | Lösungen erstellt von: | + | Lösungen erstellt von: Luka Hornung und Jan-Peter Neutert |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 34: | Zeile 34: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:auf- | + | [[Bild:auf-gab 1a.jpg|800px]] |
}} | }} | ||
| + | |||
| + | <popup name="2. Lösung"> | ||
| + | 2 der 5 Reihen bleiben frei: Ziehen ohne Reihenfolge, ohne Zurücklegen: <math>{5 \choose 2}</math><br> | ||
| + | 9 Teilnehmer auf 12 restliche Plätze verteilen: mit Reihenfolge, ohne Zurücklegen: <math>\frac {12!}{(12-9)!}</math><br> | ||
| + | <math>\Rightarrow {5 \choose 2} \cdot \frac{12!}{3!}</math> | ||
| + | </popup> | ||
| Zeile 42: | Zeile 48: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:1 b.jpg]] | + | [[Bild:1 b.jpg|800px]] |
}} | }} | ||
| Zeile 69: | Zeile 75: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:2 a.jpg]] | + | [[Bild:2 a.jpg|800px]] |
}} | }} | ||
| Zeile 76: | Zeile 82: | ||
:Wie viele Kartons muss man mindestens öffnen, um mit einer Wahrscheinlichkeit von mehr als 90 % wenigstens in einem Karton genau 4 zerbrochene Waffeln vorzufinden? | :Wie viele Kartons muss man mindestens öffnen, um mit einer Wahrscheinlichkeit von mehr als 90 % wenigstens in einem Karton genau 4 zerbrochene Waffeln vorzufinden? | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt|1= |
| − | [[Bild:2 b.jpg]] | + | '''Verbesserung der blauen Anmerkung (s. unten):'''<br /> |
| + | * man verwendet 0,0413<sup>0</sup>, da nicht <u>genau 4</u> Waffeln zerbrochen sein sollen (nicht da <u>keine</u> zerbrochen sein sollen) | ||
| + | * q = 0,9587 schließt neben dem Fall, dass <u>alle</u> okay sind auch diejenigen Fälle ein, dass <u>nicht genau 4</u> Waffeln zerbrochen sind (z.B. 1, 2, 3, 5, ...)<br /> | ||
| + | [[Bild:2 b.jpg|800px]] | ||
| + | [[Bild:2 b Teil 2.jpg|800px]] | ||
}} | }} | ||
| Zeile 85: | Zeile 95: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:2 c.jpg]] | + | [[Bild:2 c.jpg|800px]] |
}} | }} | ||
| Zeile 96: | Zeile 106: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:2 d.jpg]] | + | [[Bild:2 d.jpg|800px]] |
}} | }} | ||
| Zeile 117: | Zeile 127: | ||
:a)Roberto notiert nur, wie oft jede Sorte gewünscht wird. Wie viele Möglichkeiten gibt es dafür? | :a)Roberto notiert nur, wie oft jede Sorte gewünscht wird. Wie viele Möglichkeiten gibt es dafür? | ||
| + | <popup name="Tipp"> | ||
| + | Es handelt sich um den '''3. Fall''': Reihenfolge wird nicht berücksichtigt, jedoch mit Wiederholung (d.h. die 3 Eissorten müssen ja mehrmals gewünscht werden):<br /> | ||
| + | <math>{n+k-1 \choose k}</math> | ||
| + | </popup> <br /> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:3 a.jpg]] | + | [[Bild:3 a.jpg|800px]] |
}} | }} | ||
| Zeile 126: | Zeile 140: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:3 b.jpg]] | + | [[Bild:3 b.jpg|800px]] |
| + | [[Bild:3 b Teil2.jpg|800px]] | ||
}} | }} | ||
| + | |||
| + | <popup name="Bemerkung"> | ||
| + | '''zur einfacheren Lösung:'''<br> | ||
| + | Mississippi: <math>\Omega = \frac{12!}{8! \cdot 2! \cdot 2!} = 2970</math><br> | ||
| + | jeder das gewünschte Eis: 1 Möglichkeit<br> | ||
| + | relative WS: <math>\frac{1}{2970} \approx 0,03%. | ||
| + | |||
| + | </popup> | ||
| Zeile 151: | Zeile 174: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:4 a.jpg]] | + | [[Bild:4 a.jpg|800px]] |
}} | }} | ||
| Zeile 159: | Zeile 182: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:4 b.jpg]] | + | [[Bild:4 b.jpg|800px]] |
| + | [[Bild:4 b Teil2.jpg|800px]] | ||
}} | }} | ||
Aktuelle Version vom 7. April 2010, 11:49 Uhr
|
|
Im Raum, in dem die Abiturprüfungen für die Leistungskurse eines Gymnasiums abgehalten werden, befinden sich 20 Plätze, die in 5 Reihen zu je 4 Plätzen angeordnet sind. In jeder Reihe ist ein Fensterplatz.
|
Nach der Durchführung des Tests spendiert Roberto jedem der 12 Kollegiaten eine Riesenkugel Eis, wobei jeder zwischen den Geschmacksrichtungen Erdbeere, Vanille und Schokolade wählen kann.
|
Roberto hat sich ein Rabattsystem für seine Stammkunden ausgedacht, bei dem die Höhe des Rabatts durch gleichzeitiges Werfen von zwei gleichen Laplace-Würfeln bestimmt wird, von denen jeder 4 gelbe und 2 rote Seitenflächen hat. Von den gelben Flächen tragen jeweils drei die Aufschrift 10% und eine 15%. Die beiden roten Flächen sind jeweils mit 15% und mit 50% beschriftet. Man bekommt genau dann einen Rabatt, wenn beide Würfel die gleiche Farbe zeigen. Die Höhe des Rabatts ist das Maximum der beiden geworfenen Prozentzahlen.
|

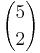
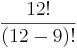
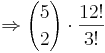





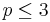 , dass also der Anteil p der zerbrochenen Waffeln gegenüber der letzten Lieferung nicht gestiegen ist.
, dass also der Anteil p der zerbrochenen Waffeln gegenüber der letzten Lieferung nicht gestiegen ist.