2007 III: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: __NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td width="800px...) |
K |
||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
<center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=2ad4ccef77e003c1a9ba1d85ca3ba82a '''Download der Originalaufgaben: Abitur 2007 LK Mathematik Bayern'''] - [[Media:LKM Abi 2007 III lös.doc|Lösungen zum Ausdrucken]]</center> | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=2ad4ccef77e003c1a9ba1d85ca3ba82a '''Download der Originalaufgaben: Abitur 2007 LK Mathematik Bayern'''] - [[Media:LKM Abi 2007 III lös.doc|Lösungen zum Ausdrucken]]</center> | ||
| + | |||
| + | |||
| + | Lösungen erstellt von: Emanuel Eirich, Ludwig Deufert und Simon Markfelder | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 34: | Zeile 37: | ||
| − | b) Wie viele Personen müssen unabhängig voneinander um einen Termin bitten, damit mit einer Wahrscheinlichkeit von mehr als 90% | + | b) Wie viele Personen müssen unabhängig voneinander um einen Termin bitten, damit mit einer Wahrscheinlichkeit von mehr als 90% mindestens einer darunter ist, der an Grauem Star leidet? |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 53: | Zeile 56: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Der Pharmakonzern Medicash forscht nach einem neuen Medikament. Es stehen 6 verschiedene Wirkstoffe zur Auswahl. Im Labor werden Testsubstanzen aus mindestens zwei Wirkstoffen gemischt, wobei von jedem beteiligten Wirkstoff jeweils genau ein Milligramm enthalten sein soll. Wie viele verschiedene Wirkstoffkombinationen sind möglich? | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_2_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 3 | ||
| + | |||
| + | Ein Labor entwickelt einen neuen Impfstoff und testet ihn in einem Tierversuch mit 900 Mäusen. Mit dem Impfstoff werden nur dann klinische Studien durchgeführt, wenn sich dabei in weniger als 2% der Fälle unerwünschte Nebenwirkungen zeigen. Bestimmen Sie für die Nullhypothese die Entscheidungsregel für den Test mit 900 Mäusen auf dem Signifikanzniveau von 1%. Verwenden Sie die Normalverteilung als Näherung. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_3_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 4 | ||
| + | |||
| + | Ein Anteil von Patienten leidet an der Infektion durch den M-Virus. Der Nachweis dieser Krankheit durch einen Bluttest ist nicht zuverlässig. Falls jemand vom M-Virus befallen ist, dann diagnostiziert der Bluttest dies nur mit einer Wahrscheinlichkeit von 90%. Falls jemand nicht infiziert ist, dann diagnostiziert der Bluttest in 5% aller Fälle trotzdem eine M-Virusinfektion. Zeigen Sie, dass die Wahrscheinlichkeit, dass eine Person tatsächlich infiziert ist, falls der Bluttest dies diagnostiziert, <math>\frac{90p}{85p + 5} | ||
| + | </math> beträgt. | ||
| + | Für welche Werte von p ist diese Wahrscheinlichkeit größer als 90%? | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_4_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 5 | ||
| + | |||
| + | In einer Spezialklinik hält sich jeder Patient (unabhängig von anderen Patienten) mindestens 3 Tage, höchstens aber 5 Tage auf. Die Verwaltung legt für die Aufenthaltsdauer X eines Patienten in Tagen folgende Wahrscheinlichkeitsverteilung zugrunde: | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | k || 3 || 4 || 5 | ||
| + | |- | ||
| + | | P(X=k) || 60% || 10% || 30% | ||
| + | |} | ||
| + | |||
| + | Jeder Patient zahlt für die Aufnahme 110€ Verwaltungsgebühr und 450€ pro Aufenthaltstag. | ||
| + | |||
| + | |||
| + | a) Bestimmen Sie den Erwartungswert und die Standardabweichung der Zufallsgröße Y: Einnahmen pro Patient (in €). | ||
| + | |||
| + | [Ergebnis: <math>E(Y) = 1775 ; \sigma = 405</math> ] | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_5a_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | b) Die Klinik benötigt jährlich mindestens 4,4 Millionen Euro Einnahmen. Mit welcher Wahrscheinlichkeit wird bei einer jährlichen Belegung von 2500 Patienten mindestens dieser Betrag erreicht? Nach dem zentralen Grenzwertsatz kann die Normalverteilung zugrunde gelegt werden. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_5b_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 6 | ||
| + | |||
| + | Bei einer Bernoulli-Kette der Länge <math>n > 1</math> und der Trefferwahrscheinlichkeit p ist die Wahrscheinlichkeit für genau 2 Treffer maximal, wenn <math>\mu = p * n = 2</math> gilt (Nachweis nicht erforderlich). | ||
| + | |||
| + | |||
| + | a) Zeigen Sie, dass für diese maximale Wahrscheinlichkeit in Abhängigkeit von n gilt: | ||
| + | |||
| + | <math>P(n) = (2 - \frac{2}{n} ) * (1 - \frac{2}{n} )^{n-2})</math> | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_6a_Lös.jpg|750px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | b) Gegen welchen Grenzwert strebt <math>P (n)</math> für <math>n \rightarrow \infty</math> ? | ||
| + | |||
| + | (Hinweis: Der Grenzwert <math>\lim_{v\to\infty} (1+\frac{k}{v})^v = e^k</math> für <math>k \in R</math> darf ohne Nachweis benutzt werden.) | ||
| + | |||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:ABI_2007_III_6b_Lös.jpg|750px]] | ||
| + | }} | ||
| − | |||
| − | |||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 23. Februar 2010, 15:27 Uhr
|
|
In einer Gemeinschaftspraxis von Augenärzten ergab eine mehrjährige Auswertung der Patientenkartei, dass im Durchschnitt jeder 15. Patient an Grauem Star leidet.
|
Der Pharmakonzern Medicash forscht nach einem neuen Medikament. Es stehen 6 verschiedene Wirkstoffe zur Auswahl. Im Labor werden Testsubstanzen aus mindestens zwei Wirkstoffen gemischt, wobei von jedem beteiligten Wirkstoff jeweils genau ein Milligramm enthalten sein soll. Wie viele verschiedene Wirkstoffkombinationen sind möglich?
|
Ein Labor entwickelt einen neuen Impfstoff und testet ihn in einem Tierversuch mit 900 Mäusen. Mit dem Impfstoff werden nur dann klinische Studien durchgeführt, wenn sich dabei in weniger als 2% der Fälle unerwünschte Nebenwirkungen zeigen. Bestimmen Sie für die Nullhypothese die Entscheidungsregel für den Test mit 900 Mäusen auf dem Signifikanzniveau von 1%. Verwenden Sie die Normalverteilung als Näherung.
|
Ein Anteil von Patienten leidet an der Infektion durch den M-Virus. Der Nachweis dieser Krankheit durch einen Bluttest ist nicht zuverlässig. Falls jemand vom M-Virus befallen ist, dann diagnostiziert der Bluttest dies nur mit einer Wahrscheinlichkeit von 90%. Falls jemand nicht infiziert ist, dann diagnostiziert der Bluttest in 5% aller Fälle trotzdem eine M-Virusinfektion. Zeigen Sie, dass die Wahrscheinlichkeit, dass eine Person tatsächlich infiziert ist, falls der Bluttest dies diagnostiziert,
|
In einer Spezialklinik hält sich jeder Patient (unabhängig von anderen Patienten) mindestens 3 Tage, höchstens aber 5 Tage auf. Die Verwaltung legt für die Aufenthaltsdauer X eines Patienten in Tagen folgende Wahrscheinlichkeitsverteilung zugrunde:
Jeder Patient zahlt für die Aufnahme 110€ Verwaltungsgebühr und 450€ pro Aufenthaltstag.
[Ergebnis:
|
Bei einer Bernoulli-Kette der Länge
(Hinweis: Der Grenzwert
|


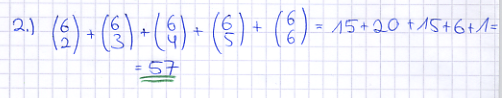

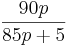 beträgt.
Für welche Werte von p ist diese Wahrscheinlichkeit größer als 90%?
beträgt.
Für welche Werte von p ist diese Wahrscheinlichkeit größer als 90%?

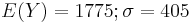 ]
]
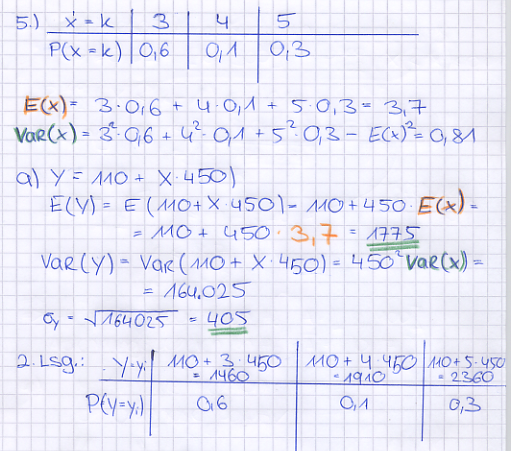

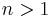 und der Trefferwahrscheinlichkeit p ist die Wahrscheinlichkeit für genau 2 Treffer maximal, wenn
und der Trefferwahrscheinlichkeit p ist die Wahrscheinlichkeit für genau 2 Treffer maximal, wenn 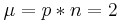 gilt (Nachweis nicht erforderlich).
gilt (Nachweis nicht erforderlich).
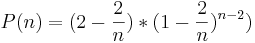
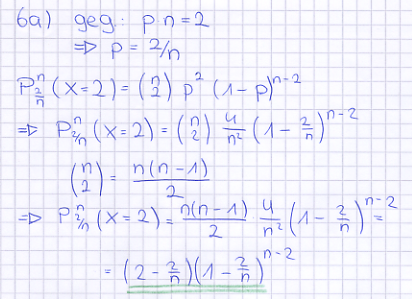
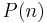 für
für 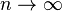 ?
?
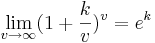 für
für 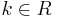 darf ohne Nachweis benutzt werden.)
darf ohne Nachweis benutzt werden.)


