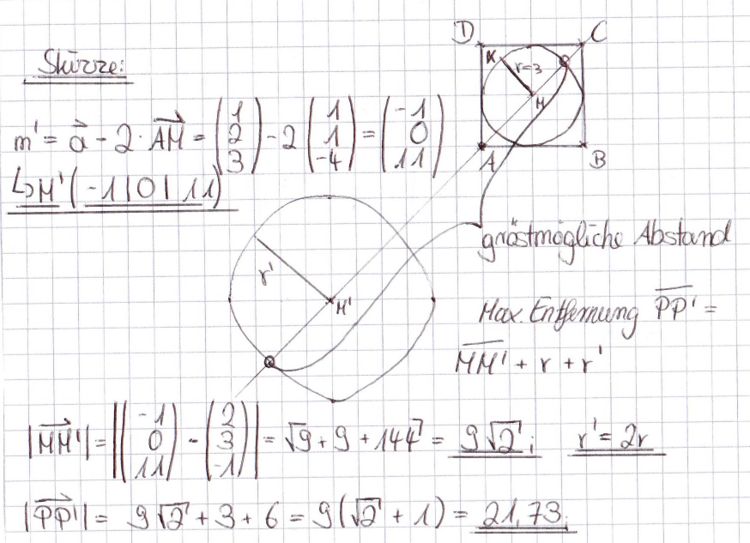2008 V: Unterschied zwischen den Versionen
| (15 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
<center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2008'''</big></center> | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2008'''</big></center> | ||
| − | <center><big>'''Analytische Geometrie | + | <center><big>'''Analytische Geometrie V'''</big></center> |
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media: | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media:2008-V-gesamt.doc|Gesamte Lösung]]</center> |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 22: | Zeile 22: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
=== Aufgabe 1 === | === Aufgabe 1 === | ||
| − | Gegeben sind in einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie S<sub>t</sub> (1-t|8|t) mit <math>t \in</math> {9} als Parameter. | + | Gegeben sind in einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie S<sub>t</sub> (1-t|8|t) mit <math>t \in</math><math>\mathbb{R} </math> \ {9} als Parameter. |
a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. ''(5 BE)'' | a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. ''(5 BE)'' | ||
| Zeile 28: | Zeile 28: | ||
Zur Kontrolle: E: 2x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>-9=0 | Zur Kontrolle: E: 2x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>-9=0 | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| − | + | * Ebene nur dann bestimmt, wenn die drei Punkte nicht auf einer Geraden liegen. | |
| − | + | * Ermittlung des Normalenvektors mit Hilfe des Vektorproduktes | |
</popup> | </popup> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:2008 | + | [[Bild:2008-V-1a.jpg|750px]] |
</popup> | </popup> | ||
| Zeile 40: | Zeile 40: | ||
Teilergebnis: M(2|3|-1) | Teilergebnis: M(2|3|-1) | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| − | + | * zz: <math>\overrightarrow { AB }</math> <math> \bot </math> <math>\overrightarrow { AD }</math> und <math>\vert</math><math>\overrightarrow { AB }</math><math>\vert</math>=<math>\vert</math> <math>\overrightarrow { AD }</math><math>\vert</math> | |
| − | + | * Mittelpunkt des Quadrats liegt bei der Hälfte der Diagonalen | |
</popup> | </popup> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:2008 | + | [[Bild:2008-V-1b.jpg|750px]] |
</popup> | </popup> | ||
c) Für welchen Wert von t ist die Entfernung von S<sub>t</sub> zu M minimal? ''(5 BE)'' | c) Für welchen Wert von t ist die Entfernung von S<sub>t</sub> zu M minimal? ''(5 BE)'' | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| − | + | * Lösung als Extremwertaufgabe | |
| − | + | * Aufstellen des Allgemeinen Geradenvektors | |
</popup> | </popup> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:2008 | + | [[Bild:2008-V-1c.jpg|750px]] |
</popup> | </popup> | ||
| Zeile 67: | Zeile 67: | ||
*Formel: V=Grundfläche <math> \cdot </math> Höhe | *Formel: V=Grundfläche <math> \cdot </math> Höhe | ||
| − | *Formel: V= <math> \vert | + | *Formel: V= <math> \vert det \overrightarrow {DA}, \overrightarrow{DC}, \overrightarrow {DS_t} \vert</math> |
Höhe des Parallelflachs ist der Abstand von S<sub>t</sub> von der Grundebene E'' | Höhe des Parallelflachs ist der Abstand von S<sub>t</sub> von der Grundebene E'' | ||
| Zeile 73: | Zeile 73: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:2008 | + | [[Bild:2008-V-2a.jpg|750px]] |
</popup> | </popup> | ||
| Zeile 80: | Zeile 80: | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| − | + | * Betrachte die Lagebeziehung von <math> \overrightarrow {DS_t} </math> bezüglich des Normalenvektors. | |
</popup> | </popup> | ||
<popup name ="Lösung"> | <popup name ="Lösung"> | ||
| − | [[Bild: 2008 | + | [[Bild: 2008-V-2b.jpg|750px]] |
</popup> | </popup> | ||
| Zeile 92: | Zeile 92: | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| − | + | * Erstelle Gerade, die senkrecht auf F steht und durch den Punkt T verläuft. | |
| − | Gerade mit Ebene E schneiden lassen; Einsetzen in die Normalenform'' | + | * Gerade mit Ebene E schneiden lassen; Einsetzen in die Normalenform'' |
</popup> | </popup> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:2008 | + | [[Bild:2008-V-2c.jpg|750px]] |
</popup> | </popup> | ||
d) Ermitteln Sie den Schnittwinkel der Ebenen E und F. ''(3 BE)'' | d) Ermitteln Sie den Schnittwinkel der Ebenen E und F. ''(3 BE)'' | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
| − | + | * Formel! | |
</popup> | </popup> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:2008 | + | [[Bild:2008-V-2d.jpg|750px]] |
</popup> | </popup> | ||
=== Aufgabe 3 === | === Aufgabe 3 === | ||
| − | K sei die Kugel, die den Punkt M aus Teilaufgabe 1b als Mittelpunkt und den | + | K sei die Kugel, die den Punkt M aus Teilaufgabe 1b als Mittelpunkt und den Radius r=3 hat. Sie wird durch eine zentrische Streckung mit A als Zentrum und dem Streckungsfaktor -2 auf die Kugel K' abgebildet. Ermitteln Sie die Koordinaten des Mittelpunkts M' von K', sowie den maximalen Abstand, den zwei Punkte P und P' haben können, wenn P auf K und P' auf K' liegt. ''(7 BE)'' |
<popup name="Tipp"> | <popup name="Tipp"> | ||
| Zeile 114: | Zeile 114: | ||
</popup> | </popup> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild: 2008 | + | [[Bild: 2008-V-3.jpg|750px]] |
</popup> | </popup> | ||
Aktuelle Version vom 10. März 2010, 16:28 Uhr
|
|
Aufgabe 1Gegeben sind in einem kartesischen Koordinatensystem des a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. (5 BE) Zur Kontrolle: E: 2x1+2x2+x3-9=0 b) Weisen Sie nach, dass sich die Punkte A, B und D durch einen vierten Punkt C zu einem Quadrat ABCD ergänzen lassen, und berechnen Sie den Diagonalenschnittpunkt M dieses Quadrats. (4 BE) Teilergebnis: M(2|3|-1) c) Für welchen Wert von t ist die Entfernung von St zu M minimal? (5 BE) Aufgabe 22) Das Quadrat ABCD als Begrenzungsfläche und die Strecke [DSt] als Seitenkante bestimmen ein Parallelflach. a) Berechnen Sie alle Werte von t, für die das Parallelflach den Rauminhalt V=144 hat. (6 BE) b) Bestimmen Sie t so, dass das Parallelflach ein Quader ist. (3 BE) Nun sei t=1. Die durch die Punkte A, D und S1 festgelegte Seitenfläche des Parallelflachs liegt in der Ebene F:2x1-x3+1=0. c) Im Punkt T(1|5|3) dieser Seitenfläche wird ein Lot errichtet. Berechnen Sie die Koordinaten des Punktes U, in dem das Lot die Ebene E schneidet, und zeigen Sie, dass U nicht im Innern des Quadrats ABCD liegt.(7 BE) d) Ermitteln Sie den Schnittwinkel der Ebenen E und F. (3 BE) Aufgabe 3K sei die Kugel, die den Punkt M aus Teilaufgabe 1b als Mittelpunkt und den Radius r=3 hat. Sie wird durch eine zentrische Streckung mit A als Zentrum und dem Streckungsfaktor -2 auf die Kugel K' abgebildet. Ermitteln Sie die Koordinaten des Mittelpunkts M' von K', sowie den maximalen Abstand, den zwei Punkte P und P' haben können, wenn P auf K und P' auf K' liegt. (7 BE)
|
 3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit
3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit 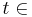

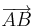
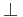
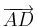 und
und 

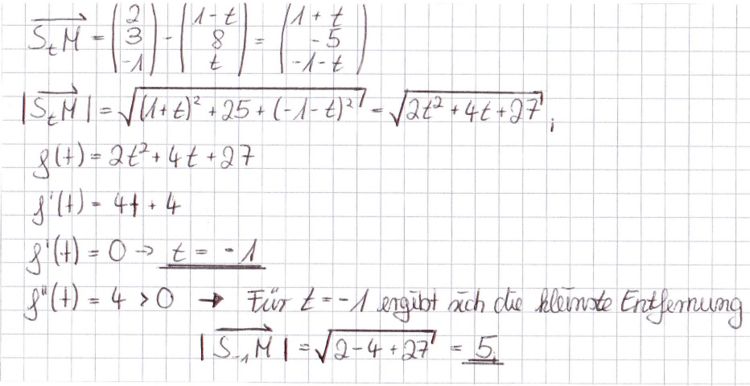
 Höhe
Höhe
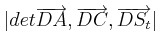

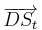 bezüglich des Normalenvektors.
bezüglich des Normalenvektors.