Symmetrie: Unterschied zwischen den Versionen
(Inhalte von Benutzerseite hierhin verschoben) |
|||
| (105 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == | + | __NOTOC__ |
| + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| + | [[Jahr der Mathematik/Gedichte|'''Gedichte''']] '''·''' [[Jahr der Mathematik/Geschichten|'''Geschichten''']] '''·''' [[Jahr der Mathematik/besondere Zahlen|'''Besondere Zahlen''']] '''·''' [[Jahr der Mathematik/Zahlen im Alltag|'''Zahlen im Alltag''']] '''·''' [[Jahr der Mathematik/Potenzen|'''Potenzen''']] '''·''' [[Jahr der Mathematik/Rap|'''Mathe-Rap''']] '''·''' [[Jahr der Mathematik/Kalender|'''Kalender''']] '''·''' [[Jahr der Mathematik/Geometrie|'''Geometrie''']] '''·''' [[Jahr der Mathematik/Symmetrie|'''Symmetrie''']] '''·''' [[Jahr der Mathematik/Quiz und Co|'''Memory, Quiz und Co. ''']] | ||
| + | </div> | ||
| + | ==Symmetrie== | ||
| − | + | Das Wort Symmetrie kommt aus dem Griechischen und bedeutet „spiegelbildlich“. | |
| − | + | Es gibt verschiedene Arten von Symmetrie. Zur Achsensymmetrie gehört immer eine Symmetrieachse (Spiegelachse), an der die Gegenstände gespiegelt werden. | |
| − | + | Symmetrie, die in der Natur vorkommt ist nicht exakt gleich (z. B. Bei Blumen oder Blättern). | |
| + | Außerdem gibt es mathematische Symmetrie (die Zahl 8, Dreieck, Quadrat, Rechteck, Raute). | ||
| + | Es gibt Dinge, die mehrere Symmetrieachsen haben, z. B. Kreise (die haben unendliche viele Symmetrieachsen). | ||
| + | |||
| + | Beispiele für Symmetrie aus dem Alltag: Dächer, Räder. | ||
| − | |||
| − | + | [[Bild:Spiegelbild02.jpg|right]] | |
| − | + | ==Wie spiegelt man einen Kreis ?== | |
| − | + | ||
| − | + | Man legt den Mittelpunkt fest und zeichnet einen Kreis mit beliebigen Radius (Abstand). | |
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Dann malt man eine Symmetrieachse und spiegelt den Mittelpunkt des Kreises an ihr. | |
| − | |||
| − | + | Nun zeichnet man mit dem gleichen Radius den gespiegelten Kreis. | |
| − | + | ==Symmetrieachsen== | |
| + | '''Wie viele Symmetrieachsen''' gibt es bei den verschiedenen Figuren? | ||
| − | + | ''Du kannst die Lösung durch Markieren des grauen Feldes sichtbar machen!'' | |
| − | + | ||
| − | + | :{| style="background-color:lightgrey; spacing:0em; padding:0em" | |
| − | + | | width="210px" height="210px" style="background-color:#FFFFFF"| | |
| − | + | <center>[[Bild:Symmetrie Klecks.jpg]]</center> | |
| − | + | ||
| − | + | ||
| − | {| style="background-color:lightgrey; spacing:0em; padding:0em" | + | |
| − | | width=" | + | |
| − | <center>[[Bild: | + | |
<center>[[Benutzer:Larissa Oppermann|Oppermann Larissa]]</center> | <center>[[Benutzer:Larissa Oppermann|Oppermann Larissa]]</center> | ||
| − | | width=" | + | | width="40px" height="50px" style="background-color:#FFFFFF"| |
<center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">1</u></span></center> | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">1</u></span></center> | ||
| − | | width=" | + | | width="210px" height="210px" style="background-color:#FFFFFF"| |
| − | <center>[[Bild: | + | <center>[[Bild:Symmetrie Florian.jpg ]]</center> |
| + | <center>[[Benutzer:Florian Rippstein|Rippstein Florian]]</center> | ||
| + | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
| + | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">2</u></span></center> | ||
| + | |||
| + | | width="210px" height="210px" style="background-color:#FFFFFF"| | ||
| + | <center>[[Bild:Symmetrie AnnaLena.jpg]]</center> | ||
<center>[[Benutzer:Anna-Lena Friedrich|Friedrich Anna-Lena]]</center> | <center>[[Benutzer:Anna-Lena Friedrich|Friedrich Anna-Lena]]</center> | ||
| − | | width=" | + | | width="40px" height="50px" style="background-color:#FFFFFF"| |
<center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">1</u></span></center> | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">1</u></span></center> | ||
|- | |- | ||
| − | | width=" | + | | width="210px" height="210px" style="background-color:#FFFFFF"| |
| − | <center>[[Bild:Symmetrie | + | <center>[[Bild:Symmetrie Chkempf1.jpg]]</center> |
| − | + | ||
<center>[[Benutzer:Christian Kempf|Kempf Christian]]</center> | <center>[[Benutzer:Christian Kempf|Kempf Christian]]</center> | ||
| width="40px" height="40px" style="background-color:#FFFFFF"| | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
<center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">2</u></span></center> | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">2</u></span></center> | ||
| − | | width=" | + | |
| − | <center>[[Bild: | + | | width="210px" height="210px" style="background-color:#FFFFFF"| |
| − | <center>[[Benutzer: | + | <center>[[Bild:Symmetrie Lukas.jpg]]</center> |
| + | <center>[[Benutzer:Lucasthebus|Lucas Thebus]]</center> | ||
| + | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
| + | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">4</u></span></center> | ||
| + | |||
| + | | width="210px" height="219px" style="background-color:#FFFFFF"| | ||
| + | <center>[[Bild:Fahnen 3.jpg]]</center> | ||
| + | <center>[[Benutzer:Lucasthebus|Lucas Thebus]]</center> | ||
| width="40px" height="40px" style="background-color:#FFFFFF"| | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
<center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">2</u></span></center> | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">2</u></span></center> | ||
| + | |||
| + | |- | ||
| + | |||
| + | | width="210px" height="210px" style="background-color:#FFFFFF"| | ||
| + | <center>[[Bild:Symmetrie Schneeflocke 1.jpg]]</center> | ||
| + | |||
| + | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
| + | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">3</u></span></center> | ||
| + | |||
| + | | width="210px" height="210px" style="background-color:#FFFFFF"| | ||
| + | <center>[[Bild:Symmetrie Schneeflocke 2.jpg]]</center> | ||
| + | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
| + | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">6</u></span></center> | ||
| + | |||
| + | | width="210px" height="219px" style="background-color:#FFFFFF"| | ||
| + | <center>[[Bild:Symmetrie Schneeflocke 3.jpg]]</center> | ||
| + | |||
| + | | width="40px" height="40px" style="background-color:#FFFFFF"| | ||
| + | <center><span style="font-size:25pt;"><u style="color:lightgrey;background:lightgrey">6</u></span></center> | ||
| + | |||
|} | |} | ||
| − | == | + | [[Bild:Photo-0003.jpg|right]] |
| + | ==Figuren mit genau drei Symmetrieachsen== | ||
| − | + | Unser Projektbeitrag ist es in ein spiegelbares Dreieck ein Muster zu malen, sodass man es aber immer noch 3 mal spiegeln kann!! | |
| + | Als erstes versuchte ich es mit einem '''O''', das hat aber nicht geklappt!! | ||
| + | Dann bin ich auf die Idee gekommen als Muster die drei '''Spiegellinien''' zu nehmen und versucht sie zu spiegeln! | ||
| + | |||
| + | '''Es hat geklappt!''' Jetzt fehlt nur noch die Farbe... | ||
| + | |||
| + | von [[Benutzer:Felix Willinger|Felix Willinger]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Fachwerkhäuser== | ||
[[Bild:Fachwerkhaus01.jpg]] | [[Bild:Fachwerkhaus01.jpg]] | ||
| + | [[Bild:Fachwerkhaus1.jpg]] | ||
| + | von [[Benutzer:Maximilian Lurz|Maximilian Lurz ]], [[Benutzer:Jan Dürr|Jan Dürr]] und [[Benutzer:Janis Suckfüll|Janis Suckfüll]] | ||
| + | '''Etwas über Fachwerkhäuser''' | ||
| − | + | Fachwerkhäuser (schweizerisch Riegelhäuser) haben im 12 Jahrhundert den Pfostenbau abgelöst und waren bis zum 19 Jahrhundert modern. | |
| + | Trotz der schlimmen Zerstörung im 2.Weltkrieg ist Deutschland immer noch führend in Anzahl von Fachwerkhäusern der verschiedensten Stilrichtungen. | ||
| + | Oftmals stehen die Häuser unter Denkmalschutz und werden von Liebhabern wegen der typischen Form verehrt. Seit den 70er Jahren fing man an die Häuser zu erneuern. | ||
| − | + | ---- | |
| − | + | '''Material:''' | |
| + | |||
| + | '''''Holzart:''''' Stieleiche, Traubeneiche oder Tanne, weil die Baumarten wasserbeständig sind. | ||
| + | |||
| + | '''''Die Zwischenräume:''''' Holzgeflecht mit Lehmbewurf ausgefüllt oder mit Backsteinen ausgemauert oder mit Lehmbausteinen verbaut und verputzt | ||
| + | |||
| + | '''''Schmuckformen:''''' Andreaskreuz, Neidköpfe, Fächerrossetten, Sonnenscheiben usw. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | '''Bezeichnungen für die Hölzer:''' | ||
| + | |||
| + | Die '''senkrechten''' Hölzer werden als '''Pfosten, Stütze''' oder als '''Ständer''' benutzt. | ||
| + | |||
| + | Die '''waagrechten''' Hölzer als '''Schwelle''' oder '''Pfette'''. | ||
| + | |||
| + | Die '''leicht schräg stehenden''' Hölzer als '''Strebe''' oder '''Schwertung'''. | ||
| + | |||
| + | Im Winkel von meist '''45 Grad''' werden die Hölzer zur Querstabilisierung '''Bänder''' genannt, (sie verbinden die senkrecht aufeinander stehenden Teile). | ||
| + | |||
| + | '''Streben''' sind meist '''symmetrisch angeordnet'''. | ||
| + | |||
| + | '''Teile die verbunden sind''' werden '''verzapft und mit Holznägel gesichert'''. | ||
| + | |||
| + | Diese Informationen stammten aus dem Wikipedia Artikel[http://de.wikipedia.org/wiki/Fachwerkhaus]. | ||
'''Noch etwas über [http://www.deutsche-fachwerkstrasse.de/de/cont.php3?s=17&c=lexikon Fachwerkhäuser]''' | '''Noch etwas über [http://www.deutsche-fachwerkstrasse.de/de/cont.php3?s=17&c=lexikon Fachwerkhäuser]''' | ||
| + | ---- | ||
'''...jetzt kommen wir aber mal zur Sache...''' | '''...jetzt kommen wir aber mal zur Sache...''' | ||
| − | Wir stellen Fachwerkhäuser nicht wegen ihrer Theorie auf unserer Seite vor, sondern wegen den Winkeln und Symmetrien, die in Fachwerken zu sehen sind. Die Winkel, die Symmetrieachsen usw., die in Fachwerken zu sehen sind, das alles ist Mathematik. | + | :Wir stellen Fachwerkhäuser nicht wegen ihrer Theorie auf unserer Seite vor, sondern wegen den Winkeln und Symmetrien, die in Fachwerken zu sehen sind. Die Winkel, die Symmetrieachsen usw., die in Fachwerken zu sehen sind, das alles ist Mathematik. |
| + | |||
| + | |||
| + | |||
| + | ==Symmetrische Flaggen und Flächen== | ||
| + | |||
| + | Wie viele Symitrieachsen haben die Fahnen? | ||
| + | |||
| + | Du kannts durch einen Klick auf das rote Feld die Lösung sichtbar machen! | ||
| + | |||
| + | Ich Lucas Thebus und Moritz Miderhoff haben uns mit Symitrie befast. An Fahnen und Flächen, dazu haben wir Fahnen und Flächen gezeichnet, wie Ihr sehen könnt: | ||
| + | |||
| + | viel Spaß beim rätzel | ||
| + | wünscht euch | ||
| + | Lucas Thebus und | ||
| + | Moritz Miderhoff | ||
| + | |||
| + | [[Bild:Flage2.jpg]] <u style="color:#F34F55;background:#F34F55">1</u> | ||
| + | |||
| + | |||
| + | [[Bild:Fahnen 5.jpg]] <u style="color:#F34F55;background:#F34F55">2</u> | ||
| + | |||
| + | |||
| + | [[Bild:Fahnen 3.jpg]] <u style="color:#F34F55;background:#F34F55">2</u> | ||
| + | |||
| + | |||
| + | [[Bild:Fahne1.jpg]] <u style="color:#F34F55;background:#F34F55">1</u> | ||
| + | |||
| + | |||
| + | |||
| + | [[Bild:Img024.jpg]] <u style="color:#F34F55;background:#F34F55">2</u> | ||
| + | |||
| + | [[Bild:Img022.jpg]] <u style="color:#F34F55;background:#F34F55">4</u> | ||
| + | |||
| + | |||
| + | von [[Benutzer:Lucasthebus|Lucas Thebus]] | ||
Aktuelle Version vom 27. September 2010, 23:38 Uhr
Gedichte · Geschichten · Besondere Zahlen · Zahlen im Alltag · Potenzen · Mathe-Rap · Kalender · Geometrie · Symmetrie · Memory, Quiz und Co.
Symmetrie
Das Wort Symmetrie kommt aus dem Griechischen und bedeutet „spiegelbildlich“.
Es gibt verschiedene Arten von Symmetrie. Zur Achsensymmetrie gehört immer eine Symmetrieachse (Spiegelachse), an der die Gegenstände gespiegelt werden.
Symmetrie, die in der Natur vorkommt ist nicht exakt gleich (z. B. Bei Blumen oder Blättern). Außerdem gibt es mathematische Symmetrie (die Zahl 8, Dreieck, Quadrat, Rechteck, Raute). Es gibt Dinge, die mehrere Symmetrieachsen haben, z. B. Kreise (die haben unendliche viele Symmetrieachsen).
Beispiele für Symmetrie aus dem Alltag: Dächer, Räder.
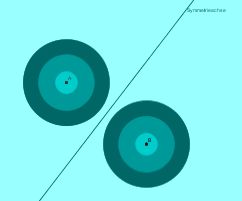
Wie spiegelt man einen Kreis ?
Man legt den Mittelpunkt fest und zeichnet einen Kreis mit beliebigen Radius (Abstand).
Dann malt man eine Symmetrieachse und spiegelt den Mittelpunkt des Kreises an ihr.
Nun zeichnet man mit dem gleichen Radius den gespiegelten Kreis.
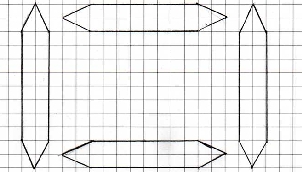
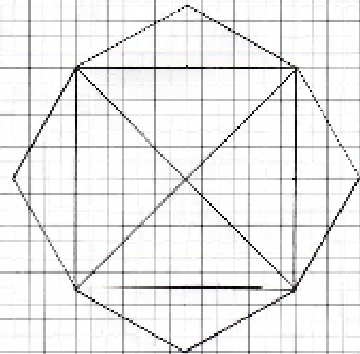
Symmetrieachsen
Wie viele Symmetrieachsen gibt es bei den verschiedenen Figuren?
Du kannst die Lösung durch Markieren des grauen Feldes sichtbar machen!

Oppermann Larissa 1 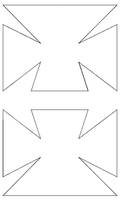
Rippstein Florian 2 
Friedrich Anna-Lena 1 
Kempf Christian 2 
Lucas Thebus 4 
Lucas Thebus 2 
3 
6 
6
Figuren mit genau drei Symmetrieachsen
Unser Projektbeitrag ist es in ein spiegelbares Dreieck ein Muster zu malen, sodass man es aber immer noch 3 mal spiegeln kann!!
Als erstes versuchte ich es mit einem O, das hat aber nicht geklappt!!
Dann bin ich auf die Idee gekommen als Muster die drei Spiegellinien zu nehmen und versucht sie zu spiegeln!
Es hat geklappt! Jetzt fehlt nur noch die Farbe...
von Felix Willinger
Fachwerkhäuser
von Maximilian Lurz , Jan Dürr und Janis Suckfüll
Etwas über Fachwerkhäuser
Fachwerkhäuser (schweizerisch Riegelhäuser) haben im 12 Jahrhundert den Pfostenbau abgelöst und waren bis zum 19 Jahrhundert modern. Trotz der schlimmen Zerstörung im 2.Weltkrieg ist Deutschland immer noch führend in Anzahl von Fachwerkhäusern der verschiedensten Stilrichtungen. Oftmals stehen die Häuser unter Denkmalschutz und werden von Liebhabern wegen der typischen Form verehrt. Seit den 70er Jahren fing man an die Häuser zu erneuern.
Material:
Holzart: Stieleiche, Traubeneiche oder Tanne, weil die Baumarten wasserbeständig sind.
Die Zwischenräume: Holzgeflecht mit Lehmbewurf ausgefüllt oder mit Backsteinen ausgemauert oder mit Lehmbausteinen verbaut und verputzt
Schmuckformen: Andreaskreuz, Neidköpfe, Fächerrossetten, Sonnenscheiben usw.
Bezeichnungen für die Hölzer:
Die senkrechten Hölzer werden als Pfosten, Stütze oder als Ständer benutzt.
Die waagrechten Hölzer als Schwelle oder Pfette.
Die leicht schräg stehenden Hölzer als Strebe oder Schwertung.
Im Winkel von meist 45 Grad werden die Hölzer zur Querstabilisierung Bänder genannt, (sie verbinden die senkrecht aufeinander stehenden Teile).
Streben sind meist symmetrisch angeordnet.
Teile die verbunden sind werden verzapft und mit Holznägel gesichert.
Diese Informationen stammten aus dem Wikipedia Artikel[1].
Noch etwas über Fachwerkhäuser
...jetzt kommen wir aber mal zur Sache...
- Wir stellen Fachwerkhäuser nicht wegen ihrer Theorie auf unserer Seite vor, sondern wegen den Winkeln und Symmetrien, die in Fachwerken zu sehen sind. Die Winkel, die Symmetrieachsen usw., die in Fachwerken zu sehen sind, das alles ist Mathematik.
Symmetrische Flaggen und Flächen
Wie viele Symitrieachsen haben die Fahnen?
Du kannts durch einen Klick auf das rote Feld die Lösung sichtbar machen!
Ich Lucas Thebus und Moritz Miderhoff haben uns mit Symitrie befast. An Fahnen und Flächen, dazu haben wir Fahnen und Flächen gezeichnet, wie Ihr sehen könnt:
viel Spaß beim rätzel
wünscht euch
Lucas Thebus und
Moritz Miderhoff
von Lucas Thebus