2009 VI: Unterschied zwischen den Versionen
(layout) |
|||
| (16 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | __NOTOC__ | |
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| − | |||
| − | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| − | + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2009'''</big></center> | |
| + | <center><big>'''Analytische Geometrie VI'''</big></center> | ||
| − | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=79e69371e73c4c671417483e9427e728 '''Download der Originalaufgaben: Abitur 2009 LK Mathematik Bayern'''] - [[Media:LKM Abi_2009_VI_Lös.doc|Lösungen zum Ausdrucken]] </center> | |
| − | :[ | + | |
| − | {{Lösung versteckt| | + | |
| + | <center>Lösungen erarbeitet von Schwarz Johanna, Lettang Theresa und Hauck Anne </center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | Gegeben sind in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Ebene F, die parallel zur x<sub>3</sub>-Achse ist und die Punkte A(-2|1,5|6) und B(0|3|0) enthält, sowie die Ebenenschar E<sub>a</sub>: 2x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>-a=0 mit a ∈ IR. | ||
| + | |||
| + | |||
| + | a) Berechnen Sie eine Gleichung der Ebene F in Normalenform. [Zur Kontrolle: F: 3x<sub>1</sub>-4x<sub>2</sub>+12=0] | ||
| + | |||
| + | :{{Lösung versteckt| | ||
[[Bild:ABI_2009_VI_a_Lös.jpg]] | [[Bild:ABI_2009_VI_a_Lös.jpg]] | ||
}} | }} | ||
| − | b) Die Kugel K mit dem Mittelpunkt M(3 | + | b) Die Kugel K mit dem Mittelpunkt M(3|-1|0) berührt die Ebene F. Berechnen Sie die Koordinaten des Berührpunkts und den Radius r der Kugel. [Teilergebnis: r=5] |
| − | + | ||
| − | {{Lösung versteckt| | + | :{{Lösung versteckt| |
[[Bild:ABI_2009_VI_b_Lös.jpg]] | [[Bild:ABI_2009_VI_b_Lös.jpg]] | ||
}} | }} | ||
| − | c) Die Punktspiegelung der Kugel K am Punkt A ergibt die Kugel K´. Bestimmen Sie die Koordinaten des Mittelpunkts M´ der Kugel K´ und geben Sie deren Radius r´ an. | + | c) Die Punktspiegelung der Kugel K am Punkt A ergibt die Kugel K´. Bestimmen Sie die Koordinaten des Mittelpunkts M´ der Kugel K´ und geben Sie deren Radius r´ an. [Teilergebnis: M´(-7|4|12)] |
| − | + | ||
| − | {{Lösung versteckt| | + | :{{Lösung versteckt| |
[[Bild:ABI_2009_VI_c_Lös.jpg]] | [[Bild:ABI_2009_VI_c_Lös.jpg]] | ||
}} | }} | ||
| Zeile 34: | Zeile 50: | ||
d) Zeigen Sie, dass die Ebenen E<sub>13</sub> und E<sub>-3</sub> symmetrisch bezüglich des Punktes A liegen, und berechnen Sie den Abstand dieser beiden Ebenen. | d) Zeigen Sie, dass die Ebenen E<sub>13</sub> und E<sub>-3</sub> symmetrisch bezüglich des Punktes A liegen, und berechnen Sie den Abstand dieser beiden Ebenen. | ||
| − | {{Lösung versteckt| | + | :{{Lösung versteckt| |
| − | [[Bild: | + | [[Bild:Abi_2009,_6,_d.jpg]]}} |
| − | }} | + | |
| + | e) Die Ebene E<sub>13</sub> schneidet die Kugel K in einem Kreis. Berechnen Sie den Mittelpunkt N und den Radius p dieses Kreises. Warum hat der Schnittkreis von E<sub>-3</sub> mit der Kugel K´ ebenfalls den Radius p? [Teilergebnis: N(5|1|1) ] | ||
| − | + | :{{Lösung versteckt| | |
| − | : | + | |
| − | + | ||
| − | {{Lösung versteckt| | + | |
[[Bild:ABI_2009_VI_e_Lös.jpg]] | [[Bild:ABI_2009_VI_e_Lös.jpg]] | ||
| + | |||
| + | [[Bild:ABI_2009_VI_e_2_Lös.jpg]] | ||
}} | }} | ||
| Zeile 49: | Zeile 64: | ||
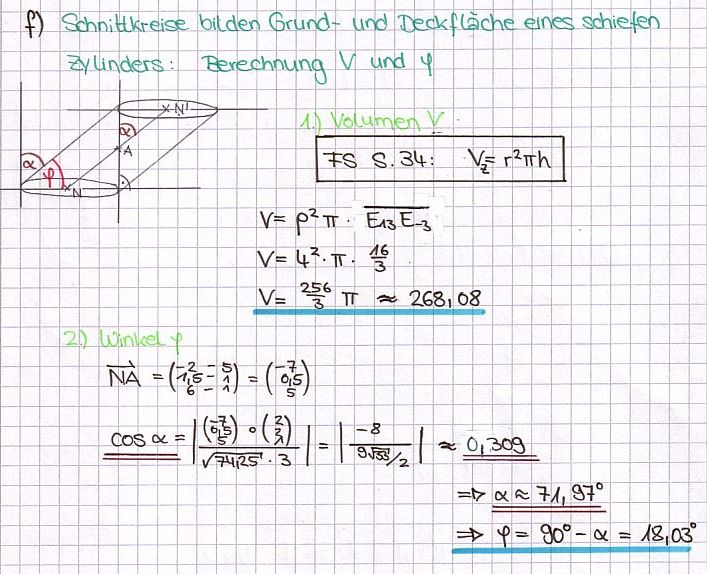
f) Die Kreise aus Teilaufgabe e bilden die Grund- und die Deckfläche eines schiefen Zylinders. Berechnen Sie das Volumen dieses schiefen Zylinders und den Winkel <math>\varphi</math> , um den die Zylinderachse gegen die Grundfläche geneigt ist. | f) Die Kreise aus Teilaufgabe e bilden die Grund- und die Deckfläche eines schiefen Zylinders. Berechnen Sie das Volumen dieses schiefen Zylinders und den Winkel <math>\varphi</math> , um den die Zylinderachse gegen die Grundfläche geneigt ist. | ||
| − | {{Lösung versteckt| | + | :{{Lösung versteckt| |
[[Bild:ABI_2009_VI_f_Lös.jpg]] | [[Bild:ABI_2009_VI_f_Lös.jpg]] | ||
}} | }} | ||
| Zeile 56: | Zeile 71: | ||
g) In welcher Ebene der Schar E<sub>a</sub> liegt der Punkt M´? Für welche Werte des Scharparameters a schneiden sich die Kugel K´ und die Ebene E<sub>a</sub> in einem Kreis? | g) In welcher Ebene der Schar E<sub>a</sub> liegt der Punkt M´? Für welche Werte des Scharparameters a schneiden sich die Kugel K´ und die Ebene E<sub>a</sub> in einem Kreis? | ||
| − | {{Lösung versteckt| | + | :{{Lösung versteckt| |
[[Bild:ABI_2009_VI_g_Lös.jpg]] | [[Bild:ABI_2009_VI_g_Lös.jpg]] | ||
}} | }} | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 22. April 2010, 17:53 Uhr
|
|
|
Gegeben sind in einem kartesischen Koordinatensystem des IR3 die Ebene F, die parallel zur x3-Achse ist und die Punkte A(-2|1,5|6) und B(0|3|0) enthält, sowie die Ebenenschar Ea: 2x1+2x2+x3-a=0 mit a ∈ IR.
e) Die Ebene E13 schneidet die Kugel K in einem Kreis. Berechnen Sie den Mittelpunkt N und den Radius p dieses Kreises. Warum hat der Schnittkreis von E-3 mit der Kugel K´ ebenfalls den Radius p? [Teilergebnis: N(5|1|1) ]
|
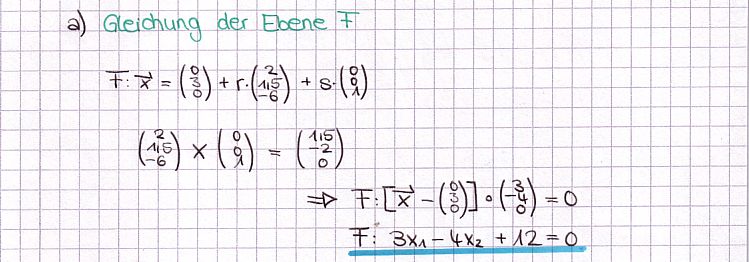





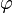 , um den die Zylinderachse gegen die Grundfläche geneigt ist.
, um den die Zylinderachse gegen die Grundfläche geneigt ist.