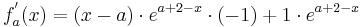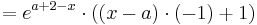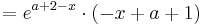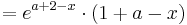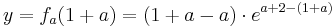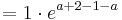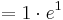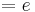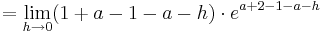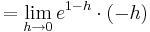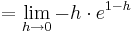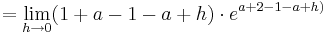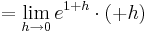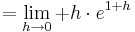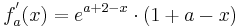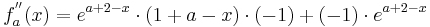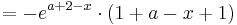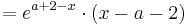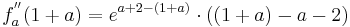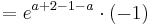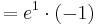Lösung: lokale Extrempunkte: Unterschied zwischen den Versionen
(→1. Möglichkeit; H-Methode) |
(→1. Möglichkeit; H-Methode) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 18: | Zeile 18: | ||
| − | Der/Die Extrempunkt/e können an der Stelle liegen, an der die erste Ableitung der Funktion | + | Der/Die Extrempunkt/e können an der Stelle liegen, an der die erste Ableitung der Funktion gleich Null ist. Die erste Ableitung einer Funktion zeigt das Steigungsverhalten dieser an. Wenn dieses gleich Null ist, besitzt die Funktion eine waagrechte Tangente an dieser Stelle. |
| − | + | Das heißt, es könnte ein Extrempunkt(Maximum / Hochpunkt und/oder Minimum / Tiefpunkt)auftreten.Dies muss jedoch erst mit der zweiten Ableitung oder mit dem Monotonieverhalten der Funktion überprüft werden, da auch ein Terassenpunkt auftreten könnte. | |
| Zeile 78: | Zeile 78: | ||
Bei diesem Extrempunkt handelt es sich um ein Maximum, da das Monotonieverhalten des Graphen von <math>f_a\,</math> kurz vor dem Extrempunkt streng monoton steigend und kurz nach dem Extrempunkt streng monoton fallend ist. | Bei diesem Extrempunkt handelt es sich um ein Maximum, da das Monotonieverhalten des Graphen von <math>f_a\,</math> kurz vor dem Extrempunkt streng monoton steigend und kurz nach dem Extrempunkt streng monoton fallend ist. | ||
| − | <u>zur Verdeutlichung</u> | + | <u>zur Verdeutlichung:</u> |
{| class="wikitable centersortable" | {| class="wikitable centersortable" | ||
| Zeile 148: | Zeile 148: | ||
| − | Falls die zweite Ableitung an dem möglichen Extrempunkt größer als Null ist, tritt ein Minimum auf. Falls sie kleiner als Null ist, handelt es | + | Falls die zweite Ableitung an dem möglichen Extrempunkt größer als Null ist, tritt ein Minimum auf. Falls sie kleiner als Null ist, handelt es sich um ein Maximum, bei gleich Null könnte ein Terrassenpunkt auftreten.<br /> |
Aktuelle Version vom 26. Januar 2010, 19:38 Uhr
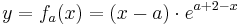 mit
mit 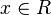 ;
; 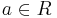
Inhaltsverzeichnis |
lokale Extrempunkte
Damit man Extrempunkte einer Funktion finden kann, braucht man ihre erste Ableitung
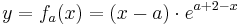
Um die erste Ableitung zu bekommen, muss man hier die Produktregel verwenden [Hilfe zur Produktregel]
Der/Die Extrempunkt/e können an der Stelle liegen, an der die erste Ableitung der Funktion gleich Null ist. Die erste Ableitung einer Funktion zeigt das Steigungsverhalten dieser an. Wenn dieses gleich Null ist, besitzt die Funktion eine waagrechte Tangente an dieser Stelle.
Das heißt, es könnte ein Extrempunkt(Maximum / Hochpunkt und/oder Minimum / Tiefpunkt)auftreten.Dies muss jedoch erst mit der zweiten Ableitung oder mit dem Monotonieverhalten der Funktion überprüft werden, da auch ein Terassenpunkt auftreten könnte.
X-Koordinate des möglichen Extrempunkts in die Funktion einsetzen, um die y-Koordinate zu erhalten.
 Möglicher Extrempunkt:
Möglicher Extrempunkt: 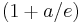
Überprüfung des Extrempunkts
1. Möglichkeit; H-Methode
Wenn es einen Vorzeichenwechsel (VZW) des Monotonieverhaltens der Funktion am möglichen Extrempunkt gibt, kann man von einem Extrempunkt sprechen.
I.
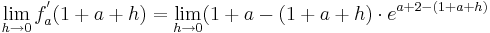
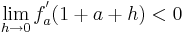
 An der Stelle
An der Stelle 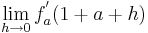 fällt der Graph (I)
fällt der Graph (I)
II.
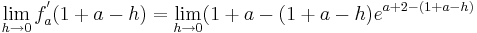
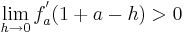
 An der Stelle
An der Stelle 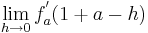 steigt der Graph (II)
steigt der Graph (II)
Aus (I) und (II) folgt:
VZW bei 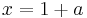
 Extrempunkt bei
Extrempunkt bei 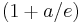
Bei diesem Extrempunkt handelt es sich um ein Maximum, da das Monotonieverhalten des Graphen von 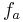 kurz vor dem Extrempunkt streng monoton steigend und kurz nach dem Extrempunkt streng monoton fallend ist.
kurz vor dem Extrempunkt streng monoton steigend und kurz nach dem Extrempunkt streng monoton fallend ist.
zur Verdeutlichung:
| x<1+a | x=1+a | x>1+a | |||
|---|---|---|---|---|---|
| ea + 2 - x | + | + | |||
| ( 1 + a - x ) | + | - | |||
| fa' ( x ) | + | - |
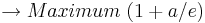
2. Möglichkeit; 2.Ableitung
Überprüfung durch die zweite Ableitung [Hilfe zur Produktregel]
Falls die zweite Ableitung an dem möglichen Extrempunkt größer als Null ist, tritt ein Minimum auf. Falls sie kleiner als Null ist, handelt es sich um ein Maximum, bei gleich Null könnte ein Terrassenpunkt auftreten.
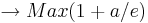
--Andre Etzel 23:49, 22. Jan. 2010 (UTC)