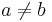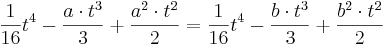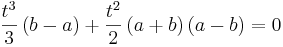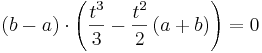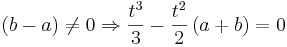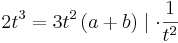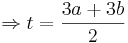Flächengleichheit: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 18: Zeile 18:
 
|width=5px|
 
|width=5px|
 
|valign="top" |
 
|valign="top" |
−
<ggb_applet width="345" height="329"  version="3.2" ggbBase64="UEsDBBQACAAIAA2YLTwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VdNb+M2ED13fwWh06ZFbEqWbAews2h3LwHS7sHtHnooQEkji41ECiSVyPvrO/yQ7TgLb9K0i6I2YFLDIWfmzZuhvHo3tA25B6W5FOsontCIgChkycV2HfWmulxG767frLYgt5ArRiqpWmbW0WySRFbe8+s33610LR8Ia5zKJw4P66hijYaI6E4BK3UNYB7JWT/whjO1+5j/CYXRhwV/yI3oerRiVI+yoi1vuR4fp85g13Dzgd/zEhRpZLGO5hm6jrNPoAwvWLOOUuolyTpKThZRNLOrtVT8sxTGqh8Or1BCiOafARFJrGw1dYGuoC8aXnImbDDOD1Qi5IGXpsYj0wyPBL6tLUDJwp9WSKnKzU4baMnwOyiJ7iSTJb3Kkln4zWYR2YWlKzqZp4tFMn4RQ3QYPUnoJF3M4ys6/qa4aVybZGm2nB0+3jTcb8AYTKUmbAA94rlVvDye3+ifZFPuU9BJLsx71pleORbEQbQxO2sLYVM2xB/FtoEgQy+LGoq7XA4bD9vMH/3rrnNbnDv59r1spCLKJgSh2oYx96PTsX7uteapU7JD7ganYs/dq8RXidNxY+5Hp9Vw4b0Locdj3DEdLXFNrAADsvwdEWlYDkiHiPSCm9vxAWlzF4KNvf4vfZtj3YzbrMIHZCkTBfhCemwl/jesUG9mNT0h5uoOlIDG008gA3rZa3Jvae6T7HwroeAtPvqFgBuzaf0NnfLSErYKgn6oTY+qW6XHFD8Rr6ajE9YHjf4XBpsMhmBsfLYHGKw/OyuZsRJbYA20gNVnHG9E34LixR4tFllraKIPhpIRZteApOslJwgfyhqX97ShjjTUUYbartPVDGeTOJCH7bCvHIfoTvtZlsFw0NONa0AtH3tny4Z1lNkZy7VsegObAvETt7JgxrVY71zoGDG1GSS4J53ZyQ77xsJOKj7AoSK/3KYODDc10kKA1q4SzXHNMYEpdrhjA+qCl7oDe7qbj9qkw6Bdve8ZgrTy6fhqYvLTxGTfNjEfq0qDsThezlIPY/KN8paGvM3j/2beBryBtb3dR9xrvOEHPLF+O1yQNcHDyJRgFOR7MvzxFml4QS4J80+JffqBsDBDWUSmT9hQ9cKVdnQw8ew4/yl+0GcWLn12Ds6jWAUUq3Mo5o9QzF+IYvV/Q7GQbctESQRrcflGGLxbWOOi5PZ9jzDqaYkexd4dwvBVzcKJqDHE0M/yCwR73/tlb8bNhTcZDH21bRVP7hO6nKRpnNJ5kr0e2di+1+2xzZ7dwZa+gy3PdbAvQp+9DvrqNdCXL4O+PAc9xU8y+3sJGN8sn5L7uQmY+xskPXvzvxD/6fErkPs/Ef5QXf8FUEsHCCoiKvDwAwAAgg0AAFBLAQIUABQACAAIAA2YLTwqIirw8AMAAIINAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAKgQAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
+
<ggb_applet width="345" height="329"  version="3.2" ggbBase64="UEsDBBQACAAIAGd6OzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vfdb9s2EH9e/wpCT82G2Pr0B2Cn2LqXYOn64K0PfRhASSeLC0UaJJXI/et7JEU7TovUQYpiGAyY1PHIu/vd747S6s3QcXIHSjMp1lEyiSMCopI1E9t11JvmchG9uXq12oLcQqkoaaTqqFlH2SSNrLxnV69+WulW3hPKncoHBvfrqKFcQ0T0TgGtdQtgTuS0HxhnVO3fl/9CZfRxwR9yLXY9WjGqR1nV1TdMh8epNdhIYQjR7BOg06mVrabOlxX0FWc1o8Lac76hEiH3rDYtup0XEWmBbVsbQzr3p1VSqnqz1wY6MnwEJddRmk4W8bJIs/G/yCKyH5eW8WSWz+dp+GGYFeXoSRpP8vksWcbhP8dNYW1S5MUiy4rFMlvOFunCm4a7DRiDaGtCB9Ah5K1i9cP5tf5N8vqA0k4yYd7SnemVS1QyijZmb21hEpUN8Vex5TDK0Muqheq2lMPGw5b5o//a79wW5065fSu5VEThhgKh2o5j6UenY/08aM1yp2SH0g1OxZ57UEmWqdNxY+lHp8WZ8N6NoSch7iQOlpgmVoABWYoFRDgtga+jd1JQE5FeMHPjJRExrLodI078pj/7rkR+h71W4XdkExUVeMKfmkq+bopxjhUCgvzRl6wDA+qFhmNveTV9RNjVLSgB3NNSIDN62WtyR3lIvnO3hop1+OgXRjypTfff6JSX1rBVMOqPZeXRdqvxQ+o/Eq+mwQnrg0b/K4PRYwjGxmfL17RS2VlNjZXYwuPQAValcXwSfQeKVQcAaWStoYl+NHRA3vUO6drAI9CP5Y7LBzrFjkyxo1JsG8aupTibJCOp6B7USYjutHeyDoZHswg6KnYstL2ODuuosDNaasl7A5sK8RM3sqLGdUfv3NhJkthmkOCePLeTfZg0bIBjpSJM7BPmkZ7Ec2S+aZEWArR2FWoe1iIVmGKHOzam3eil3oE93c2DNtlh0K4PHBiCtPLp+GZiyseJKX5sYt43jQZjcbzMcgdjlv7gvM2S/2beBrw8tb2YA+4tXs4Dnti+Hi7ImuBhZEowCvIzGf55nU3iC3JJqH9K7dMvhI4zlEVk+gUbml640o6OJs6O83vxIz6zcOOzc/A0is2IYvMUiuUJiuUzUWz+byhWsuuoqImgHS5fC4N3C+UuSmZf1QiNPS3Ro8S7Q2i6jiyciBpFDP2svECw0+Ct7E3YXHmTo6Fvtq3qcdtK4/mkmKXFy1FN7LveAdfi7O618N1r8VT3+irsxctgb14Ce/082OvvC3t4x/ySzufCPvN3Rv7kXf9M1KcPX3rcl8X49XP1GVBLBwjzZfxp0wMAAC8NAABQSwECFAAUAAgACABnejs882X8adMDAAAvDQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAA0EAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />
−
 
+
 
:'''<span style="color: darkblue">c: Flächeninhalt blau</span>,<span style="color: red"> d: Flächeninhalt rot</span>'''
 
:'''<span style="color: darkblue">c: Flächeninhalt blau</span>,<span style="color: red"> d: Flächeninhalt rot</span>'''
 
|}
 
|}
Zeile 30: Zeile 29:
 
::F<sub>a</sub> (t) = F<sub>b</sub> (t)
 
::F<sub>a</sub> (t) = F<sub>b</sub> (t)
  
−
::<math>\frac{1}{16}t^4 - \frac{a*t^3}{3} +  \frac{a^2*t^2}{2} = \frac{1}{16}t^4 - \frac{b*t^3}{3} +  \frac{b^2*t^2}{2}</math>
+
::<math>\frac{1}{16}t^4 - \frac{a\cdot t^3}{3} +  \frac{a^2\cdot t^2}{2} = \frac{1}{16}t^4 - \frac{b\cdot t^3}{3} +  \frac{b^2 \cdot t^2}{2}</math>
  
 
::<math>\frac{t^3}{3} \left( b - a \right) + \frac{t^2}{2} \left( a + b\right) \left( a - b \right) = 0</math>  
 
::<math>\frac{t^3}{3} \left( b - a \right) + \frac{t^2}{2} \left( a + b\right) \left( a - b \right) = 0</math>  
  
−
::<math>\left( b - a \right) * \left( \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) \right) = 0</math>  
+
::<math>\left( b - a \right) \cdot  \left( \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) \right) = 0</math>  
  
 
::<math>\left( b - a \right) \neq 0 \Rightarrow \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) = 0</math>
 
::<math>\left( b - a \right) \neq 0 \Rightarrow \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) = 0</math>
  
−
::<math>2 t^3 = 3 t^2 \left( a + b \right) // * \frac{1}{t^2}</math>
+
::<math>2 t^3 = 3 t^2 \left( a + b \right) \mid  \cdot \frac{1}{t^2}</math>
  
 
::<math>\Rightarrow t = \frac{3a+3b}{2} </math>
 
::<math>\Rightarrow t = \frac{3a+3b}{2} </math>
Zeile 48: Zeile 47:
  
  
 +
[[LK Mathematik Abitur NRW 2007/Schluss|Hier geht's weiter]]
  
−
 
+
[[LK Mathematik Abitur NRW 2007|Hier geht's zurück zur Übersicht]]
−
[[Facharbeit Neutert|Hier geht's zurück zur Übersicht]]
+

Aktuelle Version vom 6. Februar 2011, 15:56 Uhr

Aufgabe: Flächengleichheit zweier Funktionen

Betrachte nun zwei unterschiedliche Funktionen fa1 und fa2. Es soll der Zeitpunkt bestimmt werden, zu dem für beide Funktionsannahmen (seit t = 0) genau gleich viel Wasser durch den Fluss geflossen wäre.

Entwicklung einer Idee:
Die Aufgabe kann man sich so vorzustellen,
  • dass für zwei verschiedene a,
  • bis zu einer bestimmten Grenze, hier die gesuchte obere Grenze
  • die Flächen unter dem Graphen der jeweiligen Funktion, gleich groß sind.


Schön ist im Applet zu sehen, dass die blaue Fläche immer genauso groß ist wie die rote Fläche, obwohl die Flächen nicht deckungsgleich sind. Durch Veränderung der Schieberegler fällt auf, dass der Zeitpunkt t0 sowohl von a, als auch von b abhängig sein muss.


Nun kann man durch Gleichsetzen zweier unterschiedlicher Funktionen Fa und Fb die obere Grenze errechnen.

c: Flächeninhalt blau, d: Flächeninhalt rot
Im Weiteren wird eine Funktion mit Parameter a, die andere mit Parameter b bezeichnet. Dabei gilt:
a \neq b
Fa (t) = Fb (t)
\frac{1}{16}t^4 - \frac{a\cdot t^3}{3} + \frac{a^2\cdot t^2}{2} = \frac{1}{16}t^4 - \frac{b\cdot t^3}{3} + \frac{b^2 \cdot t^2}{2}
\frac{t^3}{3} \left( b - a \right) + \frac{t^2}{2} \left( a + b\right) \left( a - b \right) = 0
\left( b - a \right) \cdot \left( \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) \right) = 0
\left( b - a \right) \neq 0 \Rightarrow \frac{t^3}{3} - \frac{t^2}{2} \left( a + b \right) = 0
2 t^3 = 3 t^2 \left( a + b \right) \mid \cdot \frac{1}{t^2}
\Rightarrow t = \frac{3a+3b}{2}
Somit sind zwei Funktionen Fa und Fb flächenmäßig gleich groß, wenn für frei wählbares a und b gilt, dass sie bis
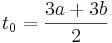t_0 = \frac{3a+3b}{2} integriert werden. Bei t0 handelt es sich um die obere Integrationsgrenze.


Hier geht's weiter

Hier geht's zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=LK_Mathematik_Abitur_NRW_2007/Flächengleichheit&oldid=40601“