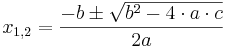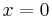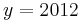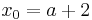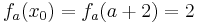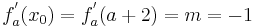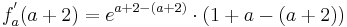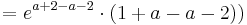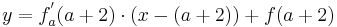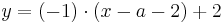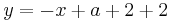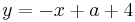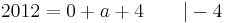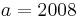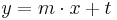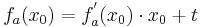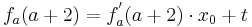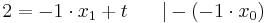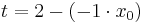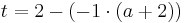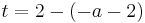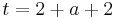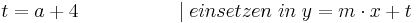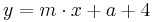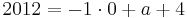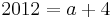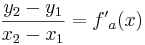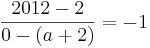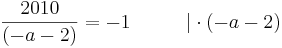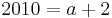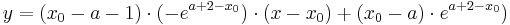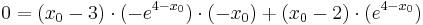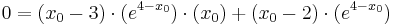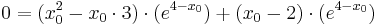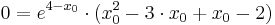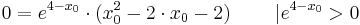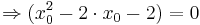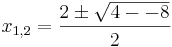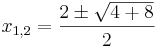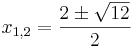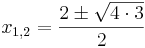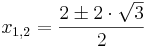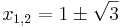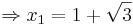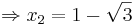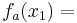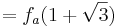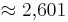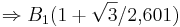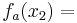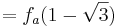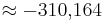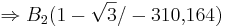Lösung von Teilaufgabe c: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f2 durch den Ursprung verläuft) |
(→Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f2 durch den Ursprung verläuft) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 130: | Zeile 130: | ||
| − | |||
| + | <ggb_applet width="615" height="522" version="3.2" ggbBase64="UEsDBBQACAAIALYJODwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VdLk9s2DD43v4Kj0247tvWw/JixN9Okl8xs2oOTHHJohpJgm12JVEVqV95fXxCkZDvbTHe3yXSag0cUAILAhw+gvHrZVSW7hUYLJddBNA4DBjJXhZC7ddCa7WgRvLx6sdqB2kHWcLZVTcXNOkjGcWDlrbh68cNK79Ud4yWZfBBwtw5M00LAdN0AL/QewDjxlpca5bztRCl4c/gt+wNyo48K5+ONrFvTO8mr4lro/nVC59WlML+IW1FAw0qVr4NZipHj6gM0RuS8XAfT0EnidRCH0zMlihKr3atG3CtprPnR+RYljGlxDwhIbGWrCeW5gjYvRSG4tMlQHGjE2J0ozN4emKJLELs9xprGofOWK9UUm4M2ULHuIzSKwhnPl0mUztJoGS+Xs1nADk6VzMfzRTqfzmfxPFmmyQIxxIAxksU4SadoukzDKQa/nOMer4pQFScp7kGLZbKYpe5ouN2AMVhJzXgHusdz14hiANy+vNGvVHkU1UpI85rXpm2IBYkXbczBnoa4NTbHn+WuBC+LsUp7yG8y1W0cbolz/e5Q0xaKJ9u9VqVqWIMbUsRq55+Ze5KNDXSwCskmJAvvwzod9IgeWdAzc0+yKoV0ofnEoz7rKOyPEZpZATq35O2xKXkGSIaAtVKY6/4FSXPjM42c/a9tlWHTnNJmcBl9JZeryWd8W91AI6F0rJJY2Fa1mt1a9rrSURwF5KLCV6fwgHBbrPcYgJMWsGugj9u1nIOLtGfM/Uy8mvRB2Bg0xpobHB2Yj7G52NY22FZ2VXBjJbZvSqgAm8oQG2RbQSPyARke2NPwiNYfFI99BDRWFI2IgZ1+0xF31H+BMDhN6j3H1TjytOAHnBenOZK3t6rwJ3s7XdJgqQSOxFFqZ2LFO+xpu+KZVmVrYJMjgvJa5dzQ6HTF9qMgCkNr29k5YxcH3EyLrejg2Gl/P3+O5DV7ZIkEranDzGkvcYlFJuRxstQuRxy3AI6AvS2rMWfq4oEhSCtXjn8sDDwszDxaxAv7m6bLcJr+t2UiMJ3kpA37q+VccZZ1h9eStjdeH+b2E8d7r6tpddFdsjW76NiI8Uv2I4PfL5CR7CfGUdJdBmzyALltK6kNglOHj67lGX5nQ+Np8IWPhC98NM++zBW6EYY4X32Kg3+bCV0Fz83l+e3g55y2zToKx/OEunWUROgC7+V791FEhu4WtFc+HZ08DaHoe0Ao7gGKx7Mw+nrwvP8ewOlHPT2fgkyuqorLgkle4TnX2JcEh7BfwYyHFh7GI0ciB0JrelXmnHkXD2C2TT6gmH27mdR/0KURVcM+nluMk370LDv0xLs/dfeYNOBP6Wy0+9YSFf5zyIV5fgXiBxUonlCB4n9WgX4MHobh+M1KMDn9nqT/XP4/59VfUEsHCBNBW6gUBAAApQ4AAFBLAQIUABQACAAIALYJODwTQVuoFAQAAKUOAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAATgQAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /><br /> | ||
| + | <br /> | ||
| + | |||
| + | <ggb_applet width="595" height="433" version="3.2" ggbBase64="UEsDBBQACAAIAM0IODwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VdLj9s2ED43v4LgabeFbVIP2wvYGzTpJcCmPTibQw4NKGlssyuRqkjtyvvrOyQlP7INuk5TtA0MQ9TMaDjzzTdDafGyq0pyD42RWi0pHzNKQOW6kGqzpK1dj+b05fWLxQb0BrJGkLVuKmGXNB5H1Mlbef3iu4XZ6gciSm/yXsLDktqmBUpM3YAozBbABvFalAblou1kKUWz+yX7DXJrDorg442qWzs4yaviRprhduL3q0tpf5L3soCGlDpf0mmKkePqPTRW5qJc0oQFSbSkEUtOlCiKnXarG/molXXmB+drlBBi5CMgIJGTLSY+zwW0eSkLKZRLxseBRoQ8yMJu0eU8RZcgN1uMNYl58JZr3RSrnbFQke4DNHpJ5+l4xtIp41HE2TROrijZBU2UJuOUzWb8apryK57EqDIYMEYSx2OUTqdJxFOWcM7xoYNqOmcpT6KYxVP8hZ3hfgXWYiENER2YAc5NI4s93u7mjXmly4Oo1lLZ16K2beNJEPeild25zRC2xqX4o9qU0MsiLNIW8rtMd6sAWxxcv9vV/hEfT7Z5rUvdkMbliVBt+msWrt7GBbq3Yt6GeYveh3O61/OryFv4axau3qqUKoTWJ86HrDkbtpGGOAE6d9wdsClFBsgFSlol7c1wg5y56zPlwf7ntsqwZ45Zs3fJv5LLxeQTui3uoFFQBlIpLGyrW0PuHXlD6XwcBeSywtug6AERrli3GECQFrBpYIg7dFyAy2vZMXE/ES8mQxAuBoOx5hYnB+ZjXS6usy12lVsVwjqJa5sSKsCesp4Nqq2gkfkeGUHdbrhF228UjfsI/FTRfkLs2dk/dMAd9Z8hDA6TeitwNe5bsRQ7HBfHOXpvb3XR79zbmdLPlUriRBylbiRWoltSvxKZ0WVrYZUjgupG58L6yRmK3U8Czpiz7dyYcYsdPuwXa9nBodP+fPwcyGu3yBIFxvgOs8e9JBQW2SOPg6UOOeK0BQgEHGxJjTn7Lt4zBGkVyvGXhYGnhZnxeTR3/yS9Ykn675bJgxkkR204nCynipOsOzyVjDvwhjDXHwUee13tVxfdJVmSi46MiLgk3xP49QIZSX4gAiXdJSWTJ8itW+XbgB47fHYtT/A7GRrnwceeCR97Ns8+zxV/IuzjfPUxon83E38UfGkuX94O/ZwzrllHbDyLfbeOYo4uppQ8hncibxhOQXfi+63j8xDi3wJC0QBQNMbXl68Hz+23AM4w6v31HGRyXVVCFUSJCve5wb70cEj3EkwEc/AQwQOJAgitHVRZcNa7eAKza/I9itl/fiYd9WLPsN1Ausdjd89JAX5XwcaE9yxZ4UdDLu3Z6Lvp5vG/fYJ+fgb6+f8J/WH+eTr/o/BPjt8j/adW/6l5/QdQSwcIg1ollA0EAACcDgAAUEsBAhQAFAAIAAgAzQg4PINaJZQNBAAAnA4AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABHBAAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
| − | <ggb_applet width=" | + | <ggb_applet width="615" height="430" version="3.2" ggbBase64="UEsDBBQACAAIAMwKODwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VdLj9s2ED43v4LQabeFbeotAfYGTXoJsGkPbnLooQEl0Ta7EqmK1K7sX98hKcmv3TTeGmjRgyFqOBzOfPPNjDx/21UleqSNZIIvHHeKHUR5LgrG1wunVatJ4ry9ezNfU7GmWUPQSjQVUQvHn3qOlrfs7s13c7kRT4iURuUzo08LRzUtdZCsG0oKuaFUWfGKlBLkpO1YyUiz/SX7g+ZK7jesjQ+8btVgJK+KeyaH15m5ry6Z+ok9soI2qBT5wolC8BxWn2mjWE7KhRNgK/EWjoeDo00Q+Xp3Ixq2E1xp9b3xFUgQkmxHARBPy+YzE+ectnnJCka4Dsb4AUoIPbFCbfSFIZikbL0BXwMvsdZyIZpiuZWKVqj7jTYCjLrJNI39NMJpFMbm2NbuBHjqJm4SxXEceGkQB+C3BIfBEw/OYBz5Qeh5aRrDEk71e3iapGnip26c4Ah0kv5u+rikSkEqJSIdlQOg64YVI+L65YN8J8q9qBaMq/ekVm1jaOD3oqXamtsc1Oggf+TrkvYyD9K0oflDJrqlBc63pn/d1uaI8SdbvxelaFADB0KIet0/M/s0OtrRUQsbHWw0ehva6Ljvpp7RMM/MPo1Wybh1rQ/cHaJ28XANk0gLwLhm74BNSTIKbHBQy5m6H16ANQ99pK7V/7mtMqiaQ96MJt0rmZzPTgg3f6ANp6WlFYfEtqKV6FHT16bO+FHQnFXwajd6QIhO1idwwEoLum7o4LetOQuX2cWH1D0Rz2eDE9oHCb7mCnoHxKN0LLq2FdSVXhVEaYkunJJWFKpKGTbwtqINy0dkiKNvgyva/iJv2ntg+oowPWJkZ39ojzvsv0AYaCf1huj6cHtakC00jMMYjbWPouhv7vVkaTpLxaAnTkLdFCvSLRyzIpkUZavoMgcE+b3IiTK90ya77wUuxlq3041GL7Zw2CxWrKP7Snu+Ae3JqzbAEk6lNBWmDmuJcEiyQR5aS21jhH5LqSXgoItqiNlU8cgQoJVNx98mhp4nJnYTL9G/IExxEP67aTJgWslBGQ6z5XjjKOoO5pLUI29wc/WFwODrarO66W7RAt10aILILfoe0d9vgJHoB0RA0t06aHaG3KrlpgycQ4Mv5tI/yeURfkdN4zL48DfCh7/Cs2PfXuaKmQijn+++eM4/jcSMgtfG8vpy6Puc1MU6wdPYN9U68V0wATN2Z7+KjKKdgnrmm6v9yxByzxG6tFb+AxAF0yBIgySK/BDHfpRatKA+oOX5PvbjKE5CPwmvh9yn/wOzhilgnpcgk4uqIrxAnFRwzz2UrIGD6S9kRLCGBxHX8suC0KphK7PGehNnMOv6H1HMXm5Xp6Pnau3+wkzs0XyObtvnuLkzNf21fncaHP2TWx1pP85YBf81cqZenxfvLC/FBXkpXpmXbyiR4RvcJiZ0r5GZoW1ux2a6O7R3zQzMDr8/zZ+0/k/q3V9QSwcIhWpWpUMEAADWDgAAUEsBAhQAFAAIAAgAzAo4PIVqVqVDBAAA1g4AAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAB9BAAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
Aktuelle Version vom 24. Januar 2010, 01:23 Uhr
Inhaltsverzeichnis |
Tangente im Punkt Wa( a + 2 / 2 ) an Gfa mit dem Schnittpunkt A (0 / 2012 )
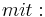
Lösung; Tangentengleichung
Tangentengleichung: siehe Formelsammlung Seite 58
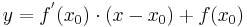
Lösung; Fußweg
Lösung; Clever
Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f2 durch den Ursprung verläuft
Verwendung der Tangentialgleichung
Lösen quadratischer Gleichungen mit Hilfe der Mitternachtsformel