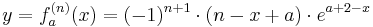Teilaufgabe e: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: === Teilaufgabe e) === Beweisen Sie, dass für die n-te Ableitung (n<u>></u>1) der Funktion f<sub>a</sub> gilt:<br /> : <math>y=f_a(x)=(-1)^{n+1}\cdot(n-x+a)\cdot e^...) |
|||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | Beweisen Sie, dass für die n-te Ableitung (<math>n\ge 1</math>) der Funktion <math>f_a\,</math> gilt:<br /> | |
| − | + | : <math>y=f_a^{(n)}(x)=(-1)^{n+1}\cdot(n-x+a)\cdot e^{a+2-x}</math> | |
| − | |||
| − | + | [[Facharbeit Andre Etzel/Teilaufgabe e/Lösung von Teilaufgabe e|Lösung von Teilaufgabe e)]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | [ | + | |
Aktuelle Version vom 23. Januar 2010, 22:22 Uhr
Beweisen Sie, dass für die n-te Ableitung (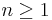 ) der Funktion
) der Funktion 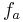 gilt:
gilt: