Lineare Gleichungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: == <span style="color: darkblue">Nullstellen</span>== == <span style="color: darkblue">y-Abschnitt</span>== == <span style="color: darkblue">Schnittpunkt zweier Geraden...) |
|||
| (111 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == <span style="color: darkblue"> | + | Mit linearen Gleichungen kann man eine Reihe von Problemen rechnerisch exakt lösen. Wir betrachten zur Veranschaulichung nun wieder die Handytarife der Firma "Smartphone". |
| − | == <span style="color: darkblue">y-Abschnitt</span>== | + | <br /><br /> |
| + | |||
| + | {|width="99%" | ||
| + | |width="40%" style="vertical-align:top"| | ||
| + | [[Bild:Handytarife.png|350px]] | ||
| + | |width="5%" style="vertical-align:top"| | ||
| + | |width="55%" style="vertical-align:center"| | ||
| + | '''<span style="color: darkorange">Verschiedene Kunden haben folgende Probleme... | ||
| + | </span>''' | ||
| + | |}<br /><br /> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == <span style="color: darkblue">Funktionswert</span>== | ||
| + | |||
| + | Herr Müller weiß aufgrund seiner bisherigen Handyrechnungen, dass er im Monat circa 2,5 Stunden mit seinem Handy telefoniert. Da er zu einem Vertrag der Firma "Smartphone" wechseln will, möchte er nun gerne wissen welcher der Tarife für seine Bedürfnisse am günstigsten ist. | ||
| + | |||
| + | → Hierzu wollen wir also herausfinden, mit welchem der Tarife bei 150 Minuten die geringsten Kosten entstehen.<br /> | ||
| + | Wir vergleichen dazu die jeweiligen '''Funktionswerte''', also die '''zu x zugehörigen y - Werte''', an der Stelle x = 150.<br /><br /><br /><br /> | ||
| + | |||
| + | <span style="color: blue">'''Tarif A'''</span>: f (x) = 0,2x<br /> | ||
| + | '''x-Wert einsetzen:''' f (150) = 0,2 · 150 = 30<br /> | ||
| + | <br /> | ||
| + | → Zur 150. Gesprächsminute liegen die Kosten bei Tarif A bei <span style="color: blue">30 €</span>.<br /><br /> | ||
| + | |||
| + | |||
| + | <span style="color: darkblue">'''Tarif C'''</span>: f(x) = <math>\begin{cases} 12, & \mbox{wenn }x\mbox{ kleiner gleich 100} \\ 0,5x - 38, & \mbox{wenn }x\mbox{ groesser 100} \end{cases} </math> | ||
| + | <br /><br /> | ||
| + | Definitionsbereich ([[Digitaler Lernpfad zu linearen Funktionen/Inhaltsverzeichnis/Grundwissensübersicht|Grundwissensübersicht]]) beachten: da 150 > 100, wählen wir zur Berechnung die Funktionsgleichung f (x) = 0,5x - 38<br /> | ||
| + | '''x-Wert einsetzen:''' f (150) = 0,5 · 150 - 38 = 37<br /> | ||
| + | <br /> | ||
| + | → Zur 150. Gesprächsminute liegen die Kosten bei Tarif C bei <span style="color: darkblue">37 €</span>.<br /><br /> | ||
| + | |||
| + | |||
| + | <span style="color: darkorange">'''Arbeitsauftrag 1:'''</span> Berechne den Funktionswert, also die anfallenden Kosten, für x = 150 bei Tarif B auf deinem Arbeitsblatt!<br /> | ||
| + | |||
| + | <span style="color: darkorange">'''Arbeitsauftrag 2:'''</span> Vergleiche nun alle Werte und entscheide, welcher der drei Tarife für Herrn Müller am geeignetsten ist!<br /><br /> | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | '''''Arbeitsauftrag 1: '''''<br /> | ||
| + | * f (150) <math>=</math> 0,3 · 150 - 10 <math>=</math> 35<br /> | ||
| + | |||
| + | '''''Arbeitsauftrag 2:'''''<br /> | ||
| + | * Die Kosten bei der 150. Gesprächsminute betragen bei Tarif A 30€, bei Tarif C 37€ und bei Tarif B 35€.<br /> | ||
| + | Demnach sollte sich Herr Müller für Tarif A entscheiden! | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | ::::::::::::::{| class="prettytable" | ||
| + | |- | ||
| + | | 1 |Um den '''Funktionswert''' (y-Wert) zu erhalten, '''x-Wert einsetzen'''. | ||
| + | |- | ||
| + | |||
| + | |}<br /><br /> | ||
| + | |||
| + | == <span style="color: darkblue">x-Wert</span>== | ||
| + | |||
| + | Frau Schmidt ist bereits Kundin bei "Smartphone" und nutzt im Moment Tarif B. Da sie sich entschieden hat im Monat künftig nicht mehr als 20 € an Handykosten ausgeben zu wollen, will sie überprüfen, ob eventuell einer der beiden anderen Tarife für sie bessere Konditionen bietet. | ||
| + | |||
| + | → Um das herauszufinden überlegen wir nun, welcher der Tarife bei 20 € die meisten Gesprächsminuten zulässt.<br /> | ||
| + | Wir suchen also die jeweiligen '''x-Werte''' an '''einer bestimmten Stelle y''' = 20.<br /><br /><br /><br /> | ||
| + | |||
| + | <span style="color: blue">'''Tarif A'''</span>: f (x) = 0,2x<br /> | ||
| + | '''y-Wert einsetzen:''' 20 = 0,2x (Bedenke, dass f (x), also der Funktionswert, gleichbedeutend mit y ist!)<br /> | ||
| + | |||
| + | '''nach x auflösen:''' x = <math>\textstyle\frac{20}{0,2}</math> = 100<br /> | ||
| + | <br /> | ||
| + | → Für 20 € kann Frau Schmidt bei Tarif A <span style="color: blue">100 Minuten</span> telefonieren.<br /><br /> | ||
| + | |||
| + | |||
| + | <span style="color: darkorange">'''Arbeitsauftrag 1:'''</span> Berechne auch die x-Werte zu den anderen beiden Tarifen auf deinem Arbeitsblatt!<br /> | ||
| + | |||
| + | <span style="color: darkorange">'''Arbeitsauftrag 2:'''</span> Welchen Tarif wird Frau Schmidt wohl wählen? | ||
| + | <br /><br /> | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | '''''Arbeitsauftrag 1:'''''<br /> | ||
| + | * Tarif B: 20 <math>=</math> 0,3x - 10; x <math>=</math> 100<br /> | ||
| + | * Tarif C: 20 <math>=</math> 0,5x - 38; x <math>=</math> 116 (Hinweis: die Gleichung 20 <math>=</math> 12 wäre nicht erfüllt) | ||
| + | |||
| + | '''''Arbeitsauftrag 2:'''''<br /> | ||
| + | * Frau Schmidt wird wahrscheinlich Tarif C wählen, da sie hier am meisten für ihr Budget telefonieren kann. | ||
| + | }} | ||
| + | |||
| + | |||
| + | ::::::::::::{| class="prettytable" | ||
| + | |- | ||
| + | | 1 |Um einen gesuchten '''x-Wert''' zu erhalten, '''y-Wert einsetzen''' und '''nach x auflösen'''. | ||
| + | |- | ||
| + | |||
| + | |}<br /><br /> | ||
| + | |||
| + | == <span style="color: darkblue">Geradengleichung</span>== | ||
| + | |||
| + | Luisa hat ihren Handyvertrag zusammen mit einem neuen Handy vor einem Jahr als Paket abgeschlossen. Weil sie die Vertragsunterlagen verlegt hat, weiß sie garnicht genau welchen der Tarife sie im Moment nutzt. Das möchte sie aber gerne herausfinden, um zu wissen wie viel sie pro Minute für das Telefonieren ausgibt. Was sie nur weiß: Ihre vorletzte Monatsrechnung betrug bei 45 Gesprächsminuten nur 3,5 €. Die letzte Monatsrechnung bei 80 min 14€. | ||
| + | |||
| + | → Um den Tarif zuzuordnen, berechnen wir eine Geradengleichung. Auch wenn weder Steigung oder y-Abschnitt gegeben sind, können wir mit den beiden gegebenen Infomationen, nämlich '''2 Punkten''' dieser Geraden zum Tarif, die '''Geradengleichung''' eindeutig ausrechnen.<br /><br /> | ||
| + | |||
| + | |||
| + | <span style="color: blue">'''Tarif A'''</span>: f (x) = 0,2x<br /> | ||
| + | Informationen: '''P<sub>1</sub>''' = (45<math>|</math>3,5); '''P<sub>2</sub>''' = (80<math>|</math>14)<br /> | ||
| + | '''mit den beiden Punkten die Steigung berechnen:''' m = <math>\textstyle\frac{\triangle y}{\triangle x}</math> = <math>\textstyle\frac{3,5 - 14}{45 - 80} </math> = <math>\textstyle\frac{-10,5}{-35} </math> = 0,3<br /> | ||
| + | y = 0,3x + t<br /> | ||
| + | |||
| + | '''einen der Punkte einsetzen, um t zu erhalten:''' (z.B: P<sub>1</sub>)<br /> | ||
| + | 3,5 = 0,3 · 45 + t; 3,5 = 13,5 + t; t = -10<br /> | ||
| + | y = 0,3x - 10<br /> | ||
| + | <br /> | ||
| + | → Luisa nutzt Tarif A mit der Gleichung <span style="color: blue">y = 0,3x - 10</span>. Ihr Minutenpreis beträgt also 0,30 €.<br /><br /> | ||
| + | |||
| + | <span style="color: darkorange">'''Arbeitsauftrag :'''</span> Berechne eine Geradengleichung mit den beiden Punkten P<sub>1</sub> (4<math>|</math>2) und P<sub>2</sub> (10<math>|</math>14)!<br /><br /> | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | '''''Arbeitsauftrag:'''''<br /> | ||
| + | * m <math>=</math> <math>\textstyle\frac{2 - 14}{4 - 10} </math> <math>=</math> <math>\textstyle\frac{-12}{-6} </math> <math>=</math> 2<br /> | ||
| + | P<sub>2</sub>: 14 <math>=</math> 2 · 10 + t; 14 <math>=</math> 20 + t; t <math>=</math> -6<br /> | ||
| + | → '''y <math>=</math> 2x - 6''' | ||
| + | }} | ||
| + | |||
| + | |||
| + | ::::::::::::{| class="prettytable" | ||
| + | |- | ||
| + | | 1 |'''Mit 2 Punkten Geradengleichung''' berechnen: <br /> | ||
| + | einen der '''Punkte in y = <math>\textstyle\frac{\triangle y}{\triangle x}</math>x + t einsetzen''' und '''nach t auflösen'''. → y = mx + t | ||
| + | |- | ||
| + | |||
| + | |}<br /><br /> | ||
| + | |||
| + | == <span style="color: darkblue">Nullstelle</span>== | ||
| + | |||
| + | Jonas entscheidet sich dafür einen Tarif ohne Grundgebühr zu wählen, weiß aber noch nicht ob Tarif A oder das Aktionsangebot Tarif B für ihn interessanter ist. Dazu möchte er erst einmal wissen wie viele kostenlose Gesprächsminuten er bei Tarif B theoretisch zur Verfügung hätte. | ||
| + | |||
| + | → Um das herauszufinden, suchen wir nun also denjenigen Punkt, an dem sich der Graph von Tarif B und die x-Achse schneiden. Links von diesem Wert befindet sich der Graph im negativen Bereich - es fallen also keine Kosten an. Rechts davon verläuft der Graph im positiven Bereich - man muss ab dieser Minute für seine Gesprächsminuten zahlen.<br /> | ||
| + | Diesen '''Schnittpunkt des Grafen mit der x-Achse''' nennt man '''Nullstelle'''!<br /><br /> | ||
| + | |||
| + | {|width="99%" | ||
| + | |width="40%" style="vertical-align:center"| | ||
| + | <span style="color: blue">'''Tarif B'''</span>: f (x) = 0,3x - 10<br /> | ||
| + | '''y = 0 setzen:''' 0 = 0,3x - 10<br /> | ||
| + | '''nach x auflösen:''' 10 = 0,3x; x = <math>\textstyle\frac{10}{0,3}</math> <math>\approx</math> = 33,3<br /> | ||
| + | <br /> | ||
| + | → Ab der 33,3. Gesrpächsminute muss man zahlen.<br /> | ||
| + | Jonas hätte also bei Tarif B ungefähr <span style="color: blue">33,3 Freiminuten</span> zur Verfügung | ||
| + | <br /><br /> | ||
| + | |width="5%" style="vertical-align:top"| | ||
| + | |width="55%" style="vertical-align:top"| | ||
| + | [[Bild:NullstelleB.png|350px]] | ||
| + | |}<br /><br /> | ||
| + | |||
| + | |||
| + | |||
| + | '''<span style="color: darkorange">Arbeitsauftrag:</span>''' Welche Geraden haben keine Nullstelle? Probiere das im GeoGebra-Applet aus!<br /> | ||
| + | |||
| + | :::::::::::::::::<ggb_applet height="400" width="900" filename="Nullstelle?.ggb" /><br /><br /> | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | '''''Arbeitsauftrag 1:'''''<br /> | ||
| + | * Nur Geraden, die zur x-Achse parallel sind, haben keine Nullstelle. Sie haben die Steigung 0 und sind daher von der Form y <math>=</math> t. Jede andere Gerade (mit der Steigung <math>\neq</math> 0) schneidet die x-Achse früher oder später! | ||
| + | }} | ||
| + | |||
| + | |||
| + | :::::::::::::{| class="prettytable" | ||
| + | |- | ||
| + | | 1 |Um die '''Nullstelle''' zu erhalten, '''y = 0 setzen''' und '''nach x auflösen'''. | ||
| + | |}<br /><br /> | ||
| + | |||
== <span style="color: darkblue">Schnittpunkt zweier Geraden</span>== | == <span style="color: darkblue">Schnittpunkt zweier Geraden</span>== | ||
| + | |||
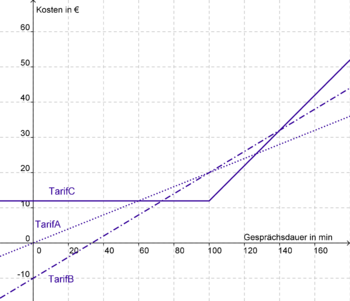
| + | Nun möchte Jonas, um sich endgültig zu entscheiden, noch herausfinden ab welcher Gesprächsdauer Tarif B teurer wird als Tarif A. | ||
| + | |||
| + | → Teurer ist Tarif B sobald sein Graph über dem von Tarif A liegt, ihn also "überholt" hat. Dies geschieht, wie man in der Grafik sieht, ab dem '''Schnittpunkt''' der beiden Graphen.<br /> | ||
| + | Hier haben die Graphen den '''gleichen Funktionswert''' (die Kosten sind identisch) und den '''gleichen x-Wert''' (bei gleicher Gesprächsdauer), rechts davon sind die Funktionswerte bzw. Kosten zu Tarif B höher.<br /><br /> | ||
| + | |||
| + | {|width="99%" | ||
| + | |width="40%" style="vertical-align:top"| | ||
| + | [[Bild:Schnittpunkt.png|350px]] | ||
| + | |width="5%" style="vertical-align:top"| | ||
| + | |width="55%" style="vertical-align:center"| | ||
| + | <span style="color: blue">'''Tarif A'''</span>: f (x) = 0,2x<br /> | ||
| + | <span style="color: blue">'''Tarif B'''</span>: f (x) = 0,3x - 10<br /> | ||
| + | '''Funktionsgleichungen gleichsetzen:''' 0,2x = 0,3x - 10<br /> | ||
| + | '''nach x auflösen:''' - 0,1x = - 10; 0,1x = 10; x = <math>\textstyle\frac{10}{0,1}</math> = 100<br /> | ||
| + | <br /> | ||
| + | → Zur 100. Gesprächsminute haben die beiden Graphen den gleichen Funktionswert,<br /> | ||
| + | man zahlt bei beiden Tarifen gleich viel.<br /> | ||
| + | <span style="color: blue">Ab der 101. Minute</span> muss man bei Tarif B mehr zahlen. | ||
| + | |}<br /><br /> | ||
| + | |||
| + | |||
| + | |||
| + | <span style="color: darkorange">'''Arbeitsauftrag:'''</span> Hat man keine Grafik vor Augen, weiß man nicht sofort, dass der Graph zu Tarif B rechts vom Schnittpunkt der beiden über dem Graphen zu Tarif A verläuft. Man kann also nicht allein anhand des Schnittpunktes entscheiden, wann Tarif B teurer ist. Überlege wie man in diesem Fall rechnerisch vorgehen könnte! | ||
| + | <br /><br /> | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | '''''Arbeitsauftrag 1:'''''<br /> | ||
| + | * Wie man rechnerisch mit solchen '''Ungleichungen''' umgeht, lernst du im nächsten Kapitel. | ||
| + | }} | ||
| + | |||
| + | ::::::::::::::{| class="prettytable" | ||
| + | |- | ||
| + | | 1 |Um den '''Schnittpunkt zweier Geraden''' zu bestimmen, <br />die '''Funktionsgleichungen gleichsetzen''' und '''nach x auflösen'''. | ||
| + | |}<br /><br /> | ||
| + | |||
| + | == <span style="color: darkblue">Zusammenfassung</span>== | ||
| + | |||
| + | '''Problemlösungen durch lineare Gleichungen'''<br /><br /> | ||
| + | |||
| + | <span style="color: blue">Jedem x- bzw. y-Wert ist ein y- bzw. x-Wert zugeordnet...</span><br /> | ||
| + | y-Wert (<span style="color: orange">'''Funktionswert'''</span>) gesucht: '''x-Wert einsetzen'''<br /> | ||
| + | <span style="color: orange">'''x-Wert'''</span> gesucht: '''y-Wert einsetzen → nach x auflösen'''<br /><br /> | ||
| + | |||
| + | <span style="color: blue">Eine Geradengleichung kann mithilfe zweier Punkte berechnet werden...</span><br /> | ||
| + | <span style="color: orange">'''Geradengleichung durch 2 Punkte'''</span> gesucht: mit beiden Punkten m mit '''m = <math>\textstyle\frac{\triangle y}{\triangle x}</math>''' berechnen → '''einen Punkt in y = <math>\textstyle\frac{\triangle y}{\triangle x}</math>x + t einsetzen → nach t auflösen''' | ||
| + | |||
| + | <span style="color: blue">Funktionsgrafen können die x-Achse schneiden ('''Nullstelle''')...</span> <small>Geraden tun dies (bis auf zur x-Achse parallele Geraden) immer!</small><br /> | ||
| + | <span style="color: orange">'''Nullstelle'''</span> gesucht: '''y = 0 setzen → nach x auflösen'''<br /><br /> | ||
| + | |||
| + | <span style="color: blue">Zwei Funktionsgrafen können sich schneiden...</span><br /> | ||
| + | <span style="color: orange">'''Schnittpunkt'''</span> gesucht: '''Gleichungen gleichsetzen → nach x auflösen'''<br /> | ||
| + | Anschließend '''y-Koordinate''' berechnen nicht vergessen! | ||
| + | <small>...gibt es für diese Gleichung keine Lösung, so existiert kein Schnittpunkt!</small> | ||
| + | |||
| + | == <span style="color: darkblue">Aufgaben</span>== | ||
| + | |||
| + | 1. Für welchen x-Wert ist der Funktionswert von f jeweils gleich 4?<br /> | ||
| + | a) f(x) = 4x + 5<br /> | ||
| + | b) f(x) = 2 + <math>\textstyle\frac{1}{4}</math> x<br /> | ||
| + | c) f(x) = 1,5x + 4<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) 4 <math>=</math> 4x + 5; '''x <math>=</math> <math>\textstyle-\frac{1}{4}</math>''' <br /> | ||
| + | b) 4 <math>=</math> 2 + <math>\textstyle\frac{1}{4}</math>x; '''x <math>=</math> 8'''<br /> | ||
| + | c) 4 <math>=</math> 1,5x + 4; '''x <math>=</math> 0''' | ||
| + | }}<br /> | ||
| + | |||
| + | 2. Bestimme die Nullstellen der Funktionen mit der Gleichung<br /> | ||
| + | a) f(x) = -3x + 12<br /> | ||
| + | b) f(x) = 4 + 0,5x<br /> | ||
| + | c) f(x) = 2x - 24<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) 0 <math>=</math> -3x + 12; '''x <math>=</math> 4''', NS (4 <math>|</math> 0)<br /> | ||
| + | b) 0 <math>=</math> 4 + 0,5x; '''x <math>=</math> -8''', NS (-8 <math>|</math> 0)<br /> | ||
| + | c) 0 <math>=</math> 2x - 24; '''x <math>=</math> 12''', NS (12 <math>|</math> 0) | ||
| + | }}<br /> | ||
| + | |||
| + | 3. Gib die Schnittpunkte der Geraden an! In welchem Quadranten liegen diese? Überprüfe dein Ergebniss zeichnerisch!<br /> | ||
| + | a) g: y <math>=</math> 2x - 3; h: y <math>=</math> x + 0,5<br /> | ||
| + | b) g: y <math>=</math> -x + 2; h: y <math>=</math> 3x + 1<br /> | ||
| + | c) g: y <math>=</math> -4x + 1; h: y <math>=</math> 2,5x - 2,25<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) <br /> | ||
| + | g <math>=</math> h; 2x - 3 <math>=</math> x + 0,5; x <math>=</math> 3,5<br /> | ||
| + | x-Wert in eine der Geradengleichungen einsetzen, um die y-Koordinate zu erhalten: g: 2 · 3,5 - 3 <math>=</math> 4<br /> | ||
| + | → '''S (3,5<math>|</math>4)'''; S liegt '''im ersten Quadranten'''!<br /> | ||
| + | |||
| + | b) <br /> | ||
| + | g <math>=</math> h; -x + 2 <math>=</math> 3x + 1; x <math>=</math> -0,25<br /> | ||
| + | h: 3 · (-0,25) + 1 <math>=</math> 0,25<br /> | ||
| + | → '''S (-0,25<math>|</math>0,25)'''; S liegt '''im zweiten Quadranten'''!<br /> | ||
| + | |||
| + | c) <br /> | ||
| + | g <math>=</math> h; -4x + 1 <math>=</math> 2,5x - 2; x <math>=</math> 0,5<br /> | ||
| + | g: -4 · 0,5 + 1 <math>=</math> -1<br /> | ||
| + | → '''S (0,5<math>|</math>-1)'''; S liegt '''im vierten Quadranten'''!<br /> | ||
| + | |||
| + | a) [[Bild:7a.png|300px]]b)[[Bild:7b.png|300px]]c)[[Bild:7c.png|300px]] | ||
| + | }}<br /> | ||
| + | |||
| + | 4. Der Graph einer linearen Funktion hat die Steigung 2 und die Nullstelle x = 4. Löse die Gleichung f(x) = 6 rechnerisch und zeichnerisch!<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | f(x) <math>=</math> 2x + t; NS (4<math>|</math>0)<br /> | ||
| + | Nullstelle einsetzen, um t zu erhalten: 0 <math>=</math> 2 · 4 + t; t <math>=</math> -8<br /> | ||
| + | → f(x) <math>=</math> 2x - 8<br /> | ||
| + | → 6 <math>=</math> 2x - 8; '''x <math>=</math> 7'''<br /> | ||
| + | [[Bild:Gleichungen4.png|300px]] | ||
| + | }}<br /> | ||
| + | |||
| + | 5. Eine Gerade geht durch den Punkt P und hat die Nullstelle x = 3. Bestimme die Geradengleichung!<br /> | ||
| + | a) P (7|4)<br /> | ||
| + | b) P (2|10)<br /> | ||
| + | c) P (0|-5)<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) <br /> | ||
| + | Die Nullstelle und der Punkt P liefern die Steigung: m <math>=</math> <math>\textstyle\frac{4-0}{7-3}</math> <math>=</math> 1<br /> | ||
| + | |||
| + | → y <math>=</math> x + t<br /> | ||
| + | Einen der beiden Punkte einsetzen, um t zu erhalten: 4 <math>=</math> 7 + t; t <math>=</math> -3<br /> | ||
| + | |||
| + | → '''y <math>=</math> x - 3'''<br /> | ||
| + | <br /> | ||
| + | b) <br /> | ||
| + | m <math>=</math> <math>\textstyle\frac{10-0}{2-3}</math> <math>=</math> -10<br /> | ||
| + | |||
| + | → y <math>=</math> -10x + t<br /> | ||
| + | 10 <math>=</math> -10 · 2 + t; t <math>=</math> 30<br /> | ||
| + | |||
| + | → '''y <math>=</math> -10x + 30'''<br /> | ||
| + | <br /> | ||
| + | c) <br /> | ||
| + | m <math>=</math> <math>\textstyle\frac{-5-0}{0-3}</math> <math>=</math> <math>\textstyle\frac{5}{3}</math><br /> | ||
| + | |||
| + | → y <math>=</math> <math>\textstyle\frac{5}{3}</math>x + t<br /> | ||
| + | -5 <math>=</math> <math>\textstyle\frac{5}{3}</math> · 0 + t; t <math>=</math> -5<br /> | ||
| + | |||
| + | → '''y <math>=</math> <math>\textstyle\frac{5}{3}</math>x - 5''' | ||
| + | }}<br /> | ||
| + | |||
| + | 6. Die Punkte A und B liegen auf dem Graphen der linearen Funktion f(x) = mx + t. Berechne die Schnittstellen des Graphen mit den Koordinatenachsen!<br /> | ||
| + | a) A (2<math>|</math>1); f(x) = x + t<br /> | ||
| + | b) A (4<math>|</math>8); B (-2<math>|</math>-6)<br /> | ||
| + | c) A (-1<math>|</math>-5); f(x) = mx - 20<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) <br /> | ||
| + | Punkt A einsetzen, um t zu erhalten: 1 <math>=</math> 2 + t; t <math>=</math> -1<br /> | ||
| + | → '''f(x) <math>=</math> x - 1'''<br /> | ||
| + | |||
| + | Schnittstelle mit der x-Achse (Nullstelle): 0 <math>=</math> x - 1; x <math>=</math> 1<br /> | ||
| + | → '''S<sub>x</sub> (0<math>|</math>1)''' <br /> | ||
| + | Schnittstelle mit der y-Achse (y-Abschnitt): f(0) <math>=</math> 0 - 1 <math>=</math> -1<br /> | ||
| + | → '''S<sub>y</sub> (0<math>|</math>-1)'''<br /> | ||
| + | Hinweis: Die Schnittstelle einer linearen Funktion mit der y-Achse, also den y-Abschnitt, kann man natürlich auch direkt aus der Funktionsgleichung ablesen. Der rechnerisch korrekte Weg ist der obige.<br /> | ||
| + | |||
| + | b) <br /> | ||
| + | Die Punkte A und B liefern die Steigung: m <math>=</math> <math>\textstyle\frac{-6-8}{-2-4}</math> <math>=</math> <math>\textstyle\frac{7}{3}</math><br />→ f(x) <math>=</math> <math>\textstyle\frac{7}{3}</math>x + t<br /> | ||
| + | Einen der beiden Punkte einsetzen, um t zu erhalten: f(4) <math>=</math> 8; 8 <math>=</math> <math>\textstyle\frac{7}{3}</math> · 4 + t; t <math>\textstyle\frac{7}{3}</math> <math>\textstyle-\frac{4}{3}</math><br /> | ||
| + | → '''f(x) <math>=</math> <math>\textstyle\frac{7}{3}</math>x - <math>\textstyle\frac{4}{3}</math>'''<br /> | ||
| + | |||
| + | Schnittstelle mit der x-Achse: 0 <math>=</math> <math>\textstyle\frac{7}{3}</math>x - <math>\textstyle\frac{4}{3}</math>; x <math>= \textstyle\frac{4}{7}</math> <br /> | ||
| + | → '''S<sub>x</sub> (<math>\textstyle\frac{4}{7} </math> <math>|</math>0)''' <br /> | ||
| + | Schnittstelle mit der y-Achse: f(0) <math>=</math> 0 - <math>\textstyle\frac{4}{3}</math> <math>=</math> <math>\textstyle-\frac{4}{3}</math><br /> | ||
| + | → '''S<sub>y</sub> (0<math>|</math>-<math>\textstyle\frac{4}{3}</math>) '''<br /> | ||
| + | |||
| + | c)<br /> | ||
| + | Punkt A in die Funktionsgleichung einsetzen, um die Steigung zu erhalten: -5 <math>=</math> m · (-1) - 20; -m <math>=</math> 15; m <math>=</math> -15<br /> | ||
| + | → f(x) <math>=</math> -15x - 20<br /> | ||
| + | |||
| + | Schnittstelle mit der x-Achse: 0 <math>=</math> -15x - 20; x <math>=</math> <math>\textstyle-\frac{4}{3}</math><br /> | ||
| + | → '''S<sub>x</sub> (<math>\textstyle\frac{4}{3}</math><math>|</math>0)''' <br /> | ||
| + | Schnittstelle mit der y-Achse: f(0) <math>=</math> 0 - 20 <math>=</math> -20<br /> | ||
| + | → '''S<sub>y</sub> (0<math>|</math>-20) ''' | ||
| + | }}<br /> | ||
| + | |||
| + | 7. Zwei Geraden g und h schneiden sich im Punkt S (-2<math>|</math>1). Die Gerade g hat die Nullstelle x = -1. Der y-Abschnitt der Geraden h ist 9.<br /> | ||
| + | Bestimme die Geradengleichungen und zeichne die Geraden!<br /> | ||
| + | |||
| + | {{Lösung versteckt| | ||
| + | * Die Nullstelle von g und der Schnittpunkt liefern die Steigung: <math>\textstyle\frac{1-0}{-2+1} = \textstyle\frac{1}{-1} =</math> -1<br />Einen der beiden Punkte einsetzen, um t zu erhalten: 0 <math>=</math> 1 + t; t <math>=</math> -1<br /> | ||
| + | → '''g: y <math>=</math> -x - 1'''<br /> | ||
| + | |||
| + | * Der y-Abschnitt und der Schnittpunkt liefern wieder die Steigung: <math>\textstyle\frac{1-9}{-2-0} = \textstyle\frac{-8}{-2} =</math> 4 | ||
| + | <br />→ '''h: y <math>=</math> 4x + 9'''<br /> | ||
| + | |||
| + | ::::::::::::[[Bild:Aufgabe 9.png|350px]] | ||
| + | }}<br /> | ||
| + | |||
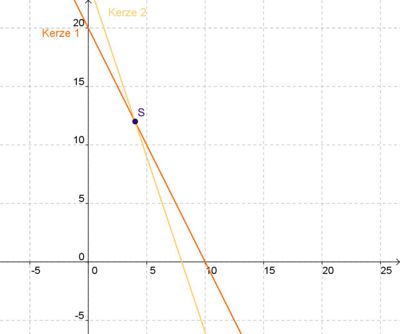
| + | 8. Eine 20 cm lange Kerze brennt in 10 Stunden ab. Eine zweite, 24 cm lange, Kerze benötigt dafür nur 8 Stunden.<br /> | ||
| + | a) Gib jeweils eine Funktionsgleichung an!<br /> | ||
| + | b) Berechne wann die Kerzen gleich lang sind, wenn diese gleichzeitig angezündet werden!<br /> | ||
| + | <br /> | ||
| + | {{Lösung versteckt| | ||
| + | a) <br /> | ||
| + | '''f<sub>1</sub>(x) <math>=</math> -2x + 20'''<br /> | ||
| + | Die Steigung -2 erhält man durch den Bruch <math>\textstyle\frac{20}{10}</math>. In 10 Stunden brennen 20 cm ab, also brennen in einer Stunde 2 cm ab (Kürzen!). Das Minuszeichen kommt durch die Überlegung, dass die Kerze an Länge verliert, der zugehörige Graf also fallen muss.<br /> | ||
| + | Da die Kerze ursprünglich 20 cm lang ist, muss dies der y-Abschnitt 20 sein.<br /> | ||
| + | |||
| + | '''f<sub>2</sub> <math>=</math> -3x + 24''' (analog der Funktionsgleichung zur ersten Kerze)<br /> | ||
| + | |||
| + | b) <br /> | ||
| + | f<sub>1</sub>(x) <math>=</math> f<sub>2</sub> (x)<br /> | ||
| + | -2x + 20 <math>=</math> -3x + 24; x <math>=</math> 4<br /> | ||
| + | x-Wert in eine Funktionsgleichung einsetzen, um y-Koordinate zu erhalten: -2 · 4 + 20 <math>=</math> 12 | ||
| + | → '''S (4<math>|</math>12)'''<br /> | ||
| + | Die beiden Kerzen sind genau '''nach 4 Stunden''' gleich lang. Sie haben dann beide eine Länge von 12 cm.<br /><br /> | ||
| + | |||
| + | Zur Veranschaulichung...<br /> | ||
| + | |||
| + | [[Bild:Kerzen.jpg|400px]] | ||
| + | }}<br /> | ||
Aktuelle Version vom 26. November 2013, 10:18 Uhr
Mit linearen Gleichungen kann man eine Reihe von Problemen rechnerisch exakt lösen. Wir betrachten zur Veranschaulichung nun wieder die Handytarife der Firma "Smartphone".
|
Verschiedene Kunden haben folgende Probleme... |
Inhaltsverzeichnis |
Funktionswert
Herr Müller weiß aufgrund seiner bisherigen Handyrechnungen, dass er im Monat circa 2,5 Stunden mit seinem Handy telefoniert. Da er zu einem Vertrag der Firma "Smartphone" wechseln will, möchte er nun gerne wissen welcher der Tarife für seine Bedürfnisse am günstigsten ist.
→ Hierzu wollen wir also herausfinden, mit welchem der Tarife bei 150 Minuten die geringsten Kosten entstehen.
Wir vergleichen dazu die jeweiligen Funktionswerte, also die zu x zugehörigen y - Werte, an der Stelle x = 150.
Tarif A: f (x) = 0,2x
x-Wert einsetzen: f (150) = 0,2 · 150 = 30
→ Zur 150. Gesprächsminute liegen die Kosten bei Tarif A bei 30 €.
Tarif C: f(x) = 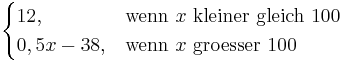
Definitionsbereich (Grundwissensübersicht) beachten: da 150 > 100, wählen wir zur Berechnung die Funktionsgleichung f (x) = 0,5x - 38
x-Wert einsetzen: f (150) = 0,5 · 150 - 38 = 37
→ Zur 150. Gesprächsminute liegen die Kosten bei Tarif C bei 37 €.
Arbeitsauftrag 1: Berechne den Funktionswert, also die anfallenden Kosten, für x = 150 bei Tarif B auf deinem Arbeitsblatt!
Arbeitsauftrag 2: Vergleiche nun alle Werte und entscheide, welcher der drei Tarife für Herrn Müller am geeignetsten ist!
Arbeitsauftrag 1:
- f (150)
 0,3 · 150 - 10
0,3 · 150 - 10  35
35
Arbeitsauftrag 2:
- Die Kosten bei der 150. Gesprächsminute betragen bei Tarif A 30€, bei Tarif C 37€ und bei Tarif B 35€.
Demnach sollte sich Herr Müller für Tarif A entscheiden!
Um den Funktionswert (y-Wert) zu erhalten, x-Wert einsetzen.
x-Wert
Frau Schmidt ist bereits Kundin bei "Smartphone" und nutzt im Moment Tarif B. Da sie sich entschieden hat im Monat künftig nicht mehr als 20 € an Handykosten ausgeben zu wollen, will sie überprüfen, ob eventuell einer der beiden anderen Tarife für sie bessere Konditionen bietet.
→ Um das herauszufinden überlegen wir nun, welcher der Tarife bei 20 € die meisten Gesprächsminuten zulässt.
Wir suchen also die jeweiligen x-Werte an einer bestimmten Stelle y = 20.
Tarif A: f (x) = 0,2x
y-Wert einsetzen: 20 = 0,2x (Bedenke, dass f (x), also der Funktionswert, gleichbedeutend mit y ist!)
nach x auflösen: x = 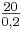 = 100
= 100
→ Für 20 € kann Frau Schmidt bei Tarif A 100 Minuten telefonieren.
Arbeitsauftrag 1: Berechne auch die x-Werte zu den anderen beiden Tarifen auf deinem Arbeitsblatt!
Arbeitsauftrag 2: Welchen Tarif wird Frau Schmidt wohl wählen?
Arbeitsauftrag 1:
- Tarif B: 20
 0,3x - 10; x
0,3x - 10; x  100
100
- Tarif C: 20
 0,5x - 38; x
0,5x - 38; x  116 (Hinweis: die Gleichung 20
116 (Hinweis: die Gleichung 20  12 wäre nicht erfüllt)
12 wäre nicht erfüllt)
Arbeitsauftrag 2:
- Frau Schmidt wird wahrscheinlich Tarif C wählen, da sie hier am meisten für ihr Budget telefonieren kann.
Um einen gesuchten x-Wert zu erhalten, y-Wert einsetzen und nach x auflösen.
Geradengleichung
Luisa hat ihren Handyvertrag zusammen mit einem neuen Handy vor einem Jahr als Paket abgeschlossen. Weil sie die Vertragsunterlagen verlegt hat, weiß sie garnicht genau welchen der Tarife sie im Moment nutzt. Das möchte sie aber gerne herausfinden, um zu wissen wie viel sie pro Minute für das Telefonieren ausgibt. Was sie nur weiß: Ihre vorletzte Monatsrechnung betrug bei 45 Gesprächsminuten nur 3,5 €. Die letzte Monatsrechnung bei 80 min 14€.
→ Um den Tarif zuzuordnen, berechnen wir eine Geradengleichung. Auch wenn weder Steigung oder y-Abschnitt gegeben sind, können wir mit den beiden gegebenen Infomationen, nämlich 2 Punkten dieser Geraden zum Tarif, die Geradengleichung eindeutig ausrechnen.
Tarif A: f (x) = 0,2x
Informationen: P1 = (45 3,5); P2 = (80
3,5); P2 = (80 14)
14)
mit den beiden Punkten die Steigung berechnen: m = 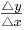 =
= 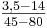 =
= 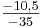 = 0,3
= 0,3
y = 0,3x + t
einen der Punkte einsetzen, um t zu erhalten: (z.B: P1)
3,5 = 0,3 · 45 + t; 3,5 = 13,5 + t; t = -10
y = 0,3x - 10
→ Luisa nutzt Tarif A mit der Gleichung y = 0,3x - 10. Ihr Minutenpreis beträgt also 0,30 €.
Arbeitsauftrag : Berechne eine Geradengleichung mit den beiden Punkten P1 (4 2) und P2 (10
2) und P2 (10 14)!
14)!
Arbeitsauftrag:
- m

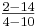

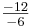
 2
2
P2: 14  2 · 10 + t; 14
2 · 10 + t; 14  20 + t; t
20 + t; t  -6
-6
→ y  2x - 6
2x - 6
Mit 2 Punkten Geradengleichung berechnen:
einen der Punkte in y =
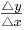 x + t einsetzen und nach t auflösen. → y = mx + t
x + t einsetzen und nach t auflösen. → y = mx + t
Nullstelle
Jonas entscheidet sich dafür einen Tarif ohne Grundgebühr zu wählen, weiß aber noch nicht ob Tarif A oder das Aktionsangebot Tarif B für ihn interessanter ist. Dazu möchte er erst einmal wissen wie viele kostenlose Gesprächsminuten er bei Tarif B theoretisch zur Verfügung hätte.
→ Um das herauszufinden, suchen wir nun also denjenigen Punkt, an dem sich der Graph von Tarif B und die x-Achse schneiden. Links von diesem Wert befindet sich der Graph im negativen Bereich - es fallen also keine Kosten an. Rechts davon verläuft der Graph im positiven Bereich - man muss ab dieser Minute für seine Gesprächsminuten zahlen.
Diesen Schnittpunkt des Grafen mit der x-Achse nennt man Nullstelle!
|
Tarif B: f (x) = 0,3x - 10 |
Arbeitsauftrag: Welche Geraden haben keine Nullstelle? Probiere das im GeoGebra-Applet aus!
Arbeitsauftrag 1:
- Nur Geraden, die zur x-Achse parallel sind, haben keine Nullstelle. Sie haben die Steigung 0 und sind daher von der Form y
 t. Jede andere Gerade (mit der Steigung
t. Jede andere Gerade (mit der Steigung 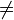 0) schneidet die x-Achse früher oder später!
0) schneidet die x-Achse früher oder später!
Um die Nullstelle zu erhalten, y = 0 setzen und nach x auflösen.
Schnittpunkt zweier Geraden
Nun möchte Jonas, um sich endgültig zu entscheiden, noch herausfinden ab welcher Gesprächsdauer Tarif B teurer wird als Tarif A.
→ Teurer ist Tarif B sobald sein Graph über dem von Tarif A liegt, ihn also "überholt" hat. Dies geschieht, wie man in der Grafik sieht, ab dem Schnittpunkt der beiden Graphen.
Hier haben die Graphen den gleichen Funktionswert (die Kosten sind identisch) und den gleichen x-Wert (bei gleicher Gesprächsdauer), rechts davon sind die Funktionswerte bzw. Kosten zu Tarif B höher.
|
Tarif A: f (x) = 0,2x |
Arbeitsauftrag: Hat man keine Grafik vor Augen, weiß man nicht sofort, dass der Graph zu Tarif B rechts vom Schnittpunkt der beiden über dem Graphen zu Tarif A verläuft. Man kann also nicht allein anhand des Schnittpunktes entscheiden, wann Tarif B teurer ist. Überlege wie man in diesem Fall rechnerisch vorgehen könnte!
Arbeitsauftrag 1:
- Wie man rechnerisch mit solchen Ungleichungen umgeht, lernst du im nächsten Kapitel.
Um den Schnittpunkt zweier Geraden zu bestimmen,
die Funktionsgleichungen gleichsetzen und nach x auflösen.
Zusammenfassung
Problemlösungen durch lineare Gleichungen
Jedem x- bzw. y-Wert ist ein y- bzw. x-Wert zugeordnet...
y-Wert (Funktionswert) gesucht: x-Wert einsetzen
x-Wert gesucht: y-Wert einsetzen → nach x auflösen
Eine Geradengleichung kann mithilfe zweier Punkte berechnet werden...
Geradengleichung durch 2 Punkte gesucht: mit beiden Punkten m mit m = 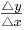 berechnen → einen Punkt in y =
berechnen → einen Punkt in y = 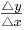 x + t einsetzen → nach t auflösen
x + t einsetzen → nach t auflösen
Funktionsgrafen können die x-Achse schneiden (Nullstelle)... Geraden tun dies (bis auf zur x-Achse parallele Geraden) immer!
Nullstelle gesucht: y = 0 setzen → nach x auflösen
Zwei Funktionsgrafen können sich schneiden...
Schnittpunkt gesucht: Gleichungen gleichsetzen → nach x auflösen
Anschließend y-Koordinate berechnen nicht vergessen!
...gibt es für diese Gleichung keine Lösung, so existiert kein Schnittpunkt!
Aufgaben
1. Für welchen x-Wert ist der Funktionswert von f jeweils gleich 4?
a) f(x) = 4x + 5
b) f(x) = 2 + 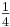 x
x
c) f(x) = 1,5x + 4
a) 4  4x + 5; x
4x + 5; x 
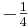
b) 4  2 +
2 + 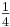 x; x
x; x  8
8
c) 4  1,5x + 4; x
1,5x + 4; x  0
0
2. Bestimme die Nullstellen der Funktionen mit der Gleichung
a) f(x) = -3x + 12
b) f(x) = 4 + 0,5x
c) f(x) = 2x - 24
a) 0  -3x + 12; x
-3x + 12; x  4, NS (4
4, NS (4  0)
0)
b) 0  4 + 0,5x; x
4 + 0,5x; x  -8, NS (-8
-8, NS (-8  0)
0)
c) 0  2x - 24; x
2x - 24; x  12, NS (12
12, NS (12  0)
0)
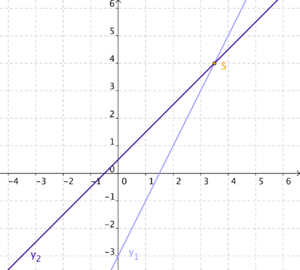
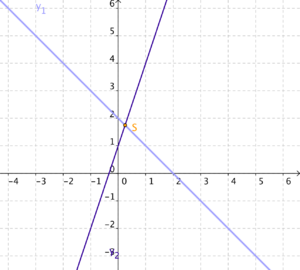
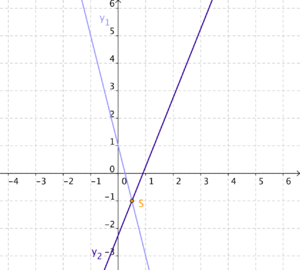
3. Gib die Schnittpunkte der Geraden an! In welchem Quadranten liegen diese? Überprüfe dein Ergebniss zeichnerisch!
a) g: y  2x - 3; h: y
2x - 3; h: y  x + 0,5
x + 0,5
b) g: y  -x + 2; h: y
-x + 2; h: y  3x + 1
3x + 1
c) g: y  -4x + 1; h: y
-4x + 1; h: y  2,5x - 2,25
2,5x - 2,25
a)
g  h; 2x - 3
h; 2x - 3  x + 0,5; x
x + 0,5; x  3,5
3,5
x-Wert in eine der Geradengleichungen einsetzen, um die y-Koordinate zu erhalten: g: 2 · 3,5 - 3  4
4
→ S (3,5 4); S liegt im ersten Quadranten!
4); S liegt im ersten Quadranten!
b)
g  h; -x + 2
h; -x + 2  3x + 1; x
3x + 1; x  -0,25
-0,25
h: 3 · (-0,25) + 1  0,25
0,25
→ S (-0,25 0,25); S liegt im zweiten Quadranten!
0,25); S liegt im zweiten Quadranten!
c)
g  h; -4x + 1
h; -4x + 1  2,5x - 2; x
2,5x - 2; x  0,5
0,5
g: -4 · 0,5 + 1  -1
-1
→ S (0,5 -1); S liegt im vierten Quadranten!
-1); S liegt im vierten Quadranten!
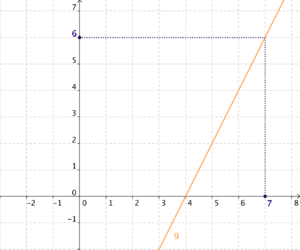
4. Der Graph einer linearen Funktion hat die Steigung 2 und die Nullstelle x = 4. Löse die Gleichung f(x) = 6 rechnerisch und zeichnerisch!
f(x)  2x + t; NS (4
2x + t; NS (4 0)
0)
Nullstelle einsetzen, um t zu erhalten: 0  2 · 4 + t; t
2 · 4 + t; t  -8
-8
→ f(x)  2x - 8
2x - 8
→ 6  2x - 8; x
2x - 8; x  7
7
5. Eine Gerade geht durch den Punkt P und hat die Nullstelle x = 3. Bestimme die Geradengleichung!
a) P (7|4)
b) P (2|10)
c) P (0|-5)
a)
Die Nullstelle und der Punkt P liefern die Steigung: m 
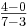
 1
1
→ y  x + t
x + t
Einen der beiden Punkte einsetzen, um t zu erhalten: 4  7 + t; t
7 + t; t  -3
-3
→ y  x - 3
x - 3
b)
m 
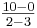
 -10
-10
→ y  -10x + t
-10x + t
10  -10 · 2 + t; t
-10 · 2 + t; t  30
30
→ y  -10x + 30
-10x + 30
c)
m 
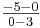

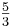
→ y 
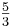 x + t
x + t
-5 
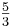 · 0 + t; t
· 0 + t; t  -5
-5
→ y 
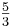 x - 5
x - 5
6. Die Punkte A und B liegen auf dem Graphen der linearen Funktion f(x) = mx + t. Berechne die Schnittstellen des Graphen mit den Koordinatenachsen!
a) A (2 1); f(x) = x + t
1); f(x) = x + t
b) A (4 8); B (-2
8); B (-2 -6)
-6)
c) A (-1 -5); f(x) = mx - 20
-5); f(x) = mx - 20
a)
Punkt A einsetzen, um t zu erhalten: 1  2 + t; t
2 + t; t  -1
-1
→ f(x)  x - 1
x - 1
Schnittstelle mit der x-Achse (Nullstelle): 0  x - 1; x
x - 1; x  1
1
→ Sx (0 1)
1)
Schnittstelle mit der y-Achse (y-Abschnitt): f(0)  0 - 1
0 - 1  -1
-1
→ Sy (0 -1)
-1)
Hinweis: Die Schnittstelle einer linearen Funktion mit der y-Achse, also den y-Abschnitt, kann man natürlich auch direkt aus der Funktionsgleichung ablesen. Der rechnerisch korrekte Weg ist der obige.
b)
Die Punkte A und B liefern die Steigung: m 
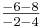

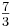
→ f(x) 
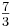 x + t
x + t
Einen der beiden Punkte einsetzen, um t zu erhalten: f(4)  8; 8
8; 8 
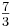 · 4 + t; t
· 4 + t; t 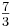
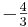
→ f(x) 
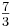 x -
x - 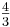
Schnittstelle mit der x-Achse: 0 
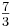 x -
x - 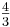 ; x
; x 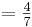
→ Sx (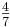
 0)
0)
Schnittstelle mit der y-Achse: f(0)  0 -
0 - 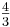

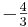
→ Sy (0 -
-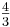 )
)
c)
Punkt A in die Funktionsgleichung einsetzen, um die Steigung zu erhalten: -5  m · (-1) - 20; -m
m · (-1) - 20; -m  15; m
15; m  -15
-15
→ f(x)  -15x - 20
-15x - 20
Schnittstelle mit der x-Achse: 0  -15x - 20; x
-15x - 20; x 
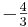
→ Sx (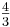
 0)
0)
Schnittstelle mit der y-Achse: f(0)  0 - 20
0 - 20  -20
-20
→ Sy (0 -20)
-20)
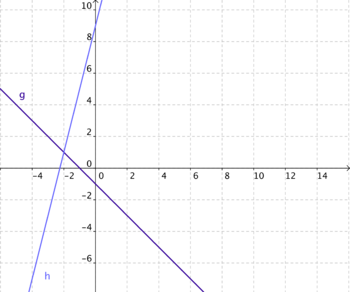
7. Zwei Geraden g und h schneiden sich im Punkt S (-2 1). Die Gerade g hat die Nullstelle x = -1. Der y-Abschnitt der Geraden h ist 9.
1). Die Gerade g hat die Nullstelle x = -1. Der y-Abschnitt der Geraden h ist 9.
Bestimme die Geradengleichungen und zeichne die Geraden!
- Die Nullstelle von g und der Schnittpunkt liefern die Steigung:
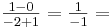 -1
-1
Einen der beiden Punkte einsetzen, um t zu erhalten: 0 1 + t; t
1 + t; t  -1
-1
→ g: y  -x - 1
-x - 1
- Der y-Abschnitt und der Schnittpunkt liefern wieder die Steigung:
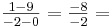 4
4
→ h: y  4x + 9
4x + 9
8. Eine 20 cm lange Kerze brennt in 10 Stunden ab. Eine zweite, 24 cm lange, Kerze benötigt dafür nur 8 Stunden.
a) Gib jeweils eine Funktionsgleichung an!
b) Berechne wann die Kerzen gleich lang sind, wenn diese gleichzeitig angezündet werden!
a)
f1(x)  -2x + 20
-2x + 20
Die Steigung -2 erhält man durch den Bruch  . In 10 Stunden brennen 20 cm ab, also brennen in einer Stunde 2 cm ab (Kürzen!). Das Minuszeichen kommt durch die Überlegung, dass die Kerze an Länge verliert, der zugehörige Graf also fallen muss.
. In 10 Stunden brennen 20 cm ab, also brennen in einer Stunde 2 cm ab (Kürzen!). Das Minuszeichen kommt durch die Überlegung, dass die Kerze an Länge verliert, der zugehörige Graf also fallen muss.
Da die Kerze ursprünglich 20 cm lang ist, muss dies der y-Abschnitt 20 sein.
f2  -3x + 24 (analog der Funktionsgleichung zur ersten Kerze)
-3x + 24 (analog der Funktionsgleichung zur ersten Kerze)
b)
f1(x)  f2 (x)
f2 (x)
-2x + 20  -3x + 24; x
-3x + 24; x  4
4
x-Wert in eine Funktionsgleichung einsetzen, um y-Koordinate zu erhalten: -2 · 4 + 20  12
→ S (4
12
→ S (4 12)
12)
Die beiden Kerzen sind genau nach 4 Stunden gleich lang. Sie haben dann beide eine Länge von 12 cm.
Zur Veranschaulichung...
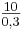
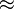 = 33,3
= 33,3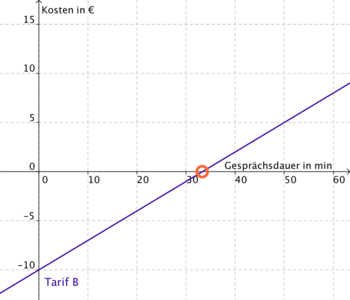
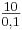 = 100
= 100