Leere Seite: Unterschied zwischen den Versionen
| Zeile 27: | Zeile 27: | ||
<div style="margin:0; margin-right:8px; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#DFF; align:left;"> | <div style="margin:0; margin-right:8px; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#DFF; align:left;"> | ||
<span style="color:#007">'''Neu: Populationsentwicklung'''</span><br> | <span style="color:#007">'''Neu: Populationsentwicklung'''</span><br> | ||
| − | + | Dieser Punkt soll folgende Fragen klären: | |
| + | * Welche '''mathematischen Grundsätze''' stecken hinter der '''zahlenmäßigen Entwicklung''' einer Population? | ||
| + | * Welche Umweltfaktoren spielen eine Rolle? | ||
| + | * Kann man das Fortpflanzungsverhalten, welches eng mit der Populationsentwicklung zusammenhängt, in unterschiedlich Kategorien einteilen? | ||
<br> | <br> | ||
| − | [[Datei: | + | '''Mathematische Grundsätze: Exponentielles Wachstum'''<br> |
| − | + | Stellt euch folgendes Beispiel vor: Vor 100 Jahren gerät ein Handelsschiff in einen Sturm, erleidet Schiffbruch und geht mitten im Meer unter. Auf dem Schiff befanden sich versteckt zwischen den Vorräten der Besatzung etliche Ratten. Nahezu alle sterben beim Sinken des Schiffes, lediglich ein Pärchen kann sich im Sturm lange genug durch die Wellen schlagen, bis es schließlich auf eine von Tieren nahezu unbewohnte Insel gespült wird. Es gibt etliche Pflanzen, die Früchte produzieren und gelegentlich nisten auch Vögel auf der Insel, von deren Eiern sich die Ratten gelegentlich welche stibitzen können. Die Ratten sind (nach einer schlimmen Odysee) letztlich in einem "Paradies" gelandet. Nehmt an, dass dieses Ratten-Paar in einem Jahr acht Jungtiere zur Welt bringt, gleich viele Männchen und Weibchen. Von dieser Familie sterben zwei Tiere (idealerweise ein Männchen und ein Weibchen) im Verlauf des Jahres z.B. weil sie zu neugierig waren. Nach einem Jahr befinden sich folglich acht Tiere auf der Insel. | |
| − | + | * Berechnet, wie viele Tiere sich nach zwei, drei, vier, fünf und sechs Jahren auf der Insel befinden, wenn sich an den Bedingungen (jeweils 8 - 2 Tiere Nachwuchs pro Paar ) ändert! | |
| − | + | * Zeichnet eine Grafik (oder lasst Excel eine Grafik zeichnen), die die Anzahl der Tiere (die "Populationsgröße") auf der Insel in Abhängigkeit von der Zeit zeigt! | |
| − | + | ||
| − | + | </div><br> | |
| + | |||
| + | <div style="border: 1px solid #FF0000; padding:7px;"> | ||
| + | {{versteckt| | ||
| + | [[Datei:PBS_Einleitung_Acetabularia.jpg|800px]]<br> | ||
| + | Es kann sein, dass ihr zu anderen Zahlenwerten gekommen seid. Entscheidend ist die Form der Kurve: Sie zeigt ein typisch '''exponentielles Wachstum'''. Die Mathematik zur Beschreibung dieser Kurve ist nicht trivial und soll hier an dieser Stelle keine große Rolle spielen. Entscheidend ist, dass ihr erkennt, welche Parameter Einfluss auf den Verlauf der Kurve haben: Die '''Anzahl der Ausgangsindividuen N<sub>0</sub>''', die '''Geburtenrate (b)''', die '''Sterberate (d)''' und die '''Zeit (t)'''. Aus der Geburten- und Sterberate lässt sich die sogenannte '''Zuwachsrate (r)''' bestimmen. Diese Größe wird später noch einmal eine wichtige Rolle spielen. | ||
| + | }} | ||
</div> | </div> | ||
| + | |||
| + | <br> | ||
| + | <div style="margin:0; margin-right:8px; border:0px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#DFF; align:left;"> | ||
| + | '''Mathematische Grundsätze: Logistisches Wachstum'''<br> | ||
| + | |||
| + | </div><br> | ||
| + | |||
| + | <div style="border: 1px solid #FF0000; padding:7px;"> | ||
| + | {{versteckt| | ||
| + | [[Datei:PBS_Einleitung_Acetabularia.jpg|800px]]<br> | ||
| + | Es kann sein, dass ihr zu anderen Zahlenwerten gekommen seid. Entscheidend ist die Form der Kurve: Sie zeigt ein typisch '''exponentielles Wachstum'''. | ||
| + | }} | ||
| + | </div> | ||
| + | |||
| + | {{#ev:youtube |GoCaakIPOrc}}<br> | ||
| + | |||
<br> | <br> | ||
Version vom 7. April 2020, 18:09 Uhr
Seite noch im Aufbau!
Wiederholung: Ökologie
Zunächst zu den Grundlagen: Bei der Thematik "Ökologie" wird gelegentlich auf Wissen aus der zehnten Jahrgangsstufe zurückgegriffen. Auch im normalen Q11-Unterricht wiederhole ich diese Grundlagen nicht ausführlich, sondern verweise lediglich auf ein Skript aus der zehnten:
Skript "Ökologie" (10. Jahrgangsstufe) als pdf-Datei
Die Hefteinträge sind zwar kurz, sollten aber verständlich sein. Es geht hauptsächlich darum, dass ihr euch unter bestimmten Begriffen etwas vorstellen und diese auch bei Erklärungen sicher verwenden könnt:
- Produzenten, Konsumenten, Destruenten
- Ökosystem, Biotop, Biozönose
- Biotische und abiotische Umweltfaktoren
Es wird im Kolloquium aber sicher keine Fragen geben: "Was bedeutet Biotop?"
- Wenn ihr zu den Vitalitätskurven etwas machen möchtet, dann könnt ihr im neuen Wiki die Einheit Biologie5 und Biologie6 auf der folgenden Seite bearbeiten: [Hier klicken]. Für einige Aufgaben ist dazu zwar das Buch aus der zehnten Jahrgangsstufe nötig, aber diese Aufgaben könnt ihr überspringen.
- Das Konkurrenzausschlussprinzip, das stark mit dem Begriff der ökologischen Nische zusammenhängt, ist für mich aus biologischer Sicht ein äußerst spannendes Prinzip. In der zehnten Jahrgangsstufe mache ich dazu viele Beispiele. Im Kolloquium habe ich jedoch noch nie darauf Bezug genommen und habe es auch nicht vor. Falls ihr trotzdem dazu mehr wissen möchtet: Das Video von simpleclub ist ganz o.k.:
- Den Punkt "Populationsschwankungen" bespreche ich in der Q11 erneut (auch in der folgenden Einheit).
Neu: Populationsentwicklung
Dieser Punkt soll folgende Fragen klären:
- Welche mathematischen Grundsätze stecken hinter der zahlenmäßigen Entwicklung einer Population?
- Welche Umweltfaktoren spielen eine Rolle?
- Kann man das Fortpflanzungsverhalten, welches eng mit der Populationsentwicklung zusammenhängt, in unterschiedlich Kategorien einteilen?
Mathematische Grundsätze: Exponentielles Wachstum
Stellt euch folgendes Beispiel vor: Vor 100 Jahren gerät ein Handelsschiff in einen Sturm, erleidet Schiffbruch und geht mitten im Meer unter. Auf dem Schiff befanden sich versteckt zwischen den Vorräten der Besatzung etliche Ratten. Nahezu alle sterben beim Sinken des Schiffes, lediglich ein Pärchen kann sich im Sturm lange genug durch die Wellen schlagen, bis es schließlich auf eine von Tieren nahezu unbewohnte Insel gespült wird. Es gibt etliche Pflanzen, die Früchte produzieren und gelegentlich nisten auch Vögel auf der Insel, von deren Eiern sich die Ratten gelegentlich welche stibitzen können. Die Ratten sind (nach einer schlimmen Odysee) letztlich in einem "Paradies" gelandet. Nehmt an, dass dieses Ratten-Paar in einem Jahr acht Jungtiere zur Welt bringt, gleich viele Männchen und Weibchen. Von dieser Familie sterben zwei Tiere (idealerweise ein Männchen und ein Weibchen) im Verlauf des Jahres z.B. weil sie zu neugierig waren. Nach einem Jahr befinden sich folglich acht Tiere auf der Insel.
- Berechnet, wie viele Tiere sich nach zwei, drei, vier, fünf und sechs Jahren auf der Insel befinden, wenn sich an den Bedingungen (jeweils 8 - 2 Tiere Nachwuchs pro Paar ) ändert!
- Zeichnet eine Grafik (oder lasst Excel eine Grafik zeichnen), die die Anzahl der Tiere (die "Populationsgröße") auf der Insel in Abhängigkeit von der Zeit zeigt!
Es kann sein, dass ihr zu anderen Zahlenwerten gekommen seid. Entscheidend ist die Form der Kurve: Sie zeigt ein typisch exponentielles Wachstum. Die Mathematik zur Beschreibung dieser Kurve ist nicht trivial und soll hier an dieser Stelle keine große Rolle spielen. Entscheidend ist, dass ihr erkennt, welche Parameter Einfluss auf den Verlauf der Kurve haben: Die Anzahl der Ausgangsindividuen N0, die Geburtenrate (b), die Sterberate (d) und die Zeit (t). Aus der Geburten- und Sterberate lässt sich die sogenannte Zuwachsrate (r) bestimmen. Diese Größe wird später noch einmal eine wichtige Rolle spielen.
Mathematische Grundsätze: Logistisches Wachstum
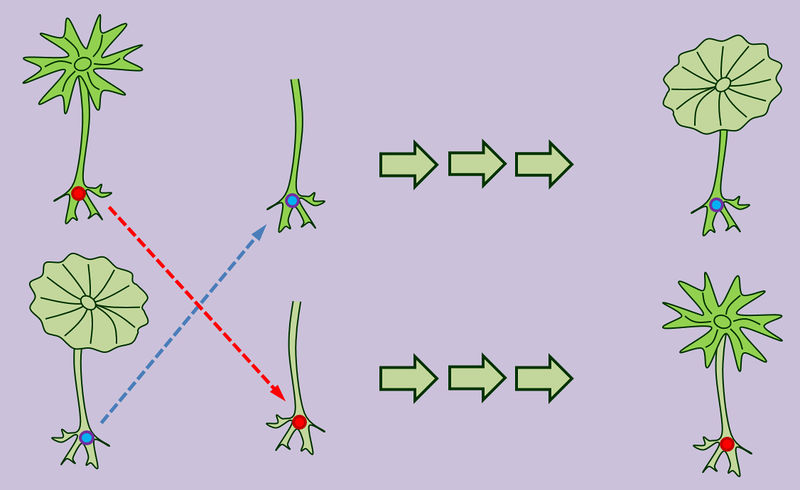
- Versuchsaufbau: Man verwendet verschiedene Arten von Acetabularia. Das sind einzellige Grünalgen, die sich vor allem in der Form ihres Hutes unterscheiden. Eine typische Eigenschaft dieser Algen ist das Nachwachsen des Hutes, wenn man ihn abschneidet. die Hüte zweier verschiedener Acetabularia-Arten wurden entfernt und die Zellkerne, die im Rhizoid sitzen vertauscht.
- Ergebnis: Es wächst (nach einigen Zwischenformen) die Hut-Form, die zum transplantierten Zellkern passt.
- Schlussfolgerung: Der Zellkern enthält die Informationen über die Merkmale der Zelle.

