Abi 2012 Analysis I Teil A: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 28: Zeile 28:
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
  
−
[[Bild:ABI2017_AI_TeilA_1ab_Lös.jpg|700px]]
+
[[Bild:ABI2012_AI_TeilA_1ab_Lös.jpg|700px]]
  
 
}}
 
}}
Zeile 49: Zeile 49:
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
  
−
[[Bild:ABI2017_AI_TeilA_2ab_Lös.jpg|700px]]
+
[[Bild:ABI2012_AI_TeilA_2ab_Lös.jpg|700px]]
  
 
}}
 
}}
Zeile 70: Zeile 70:
  
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
−
[[Bild:ABI2017_AI_TeilA_3ab_Lös.jpg|700px]]
+
[[Bild:ABI2012_AI_TeilA_3ab_Lös.jpg|700px]]
  
 
}}
 
}}
Zeile 84: Zeile 84:
  
 
;Aufgabe 4
 
;Aufgabe 4
−
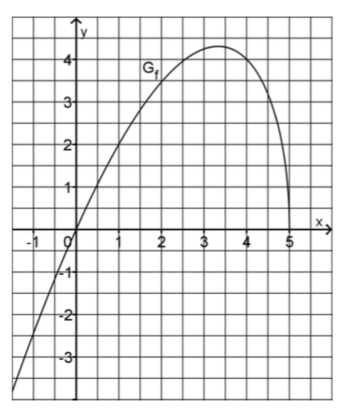
[[Datei:Abitur 2012 Teil A Aufgabengruppe I A4.png|thumb|Abitur 2012 Teil A Aufgabengruppe I A4|300px]]
+
[[Datei:Abitur 2012 Teil A Aufgabengruppe I A4.png|center|350px]]
−
Abbildung 1 zeigt den Graphen G<sub>f</sub> einer in ]-∞;5] definierten Funktion f.
+
Abbildung 1 zeigt den Graphen G<sub>f</sub> einer in ]-∞;5] definierten Funktion f.
−
Skizzieren Sie in der Abbildung den Graphen der zugehörigen Ableitungsfunktion f'. Berücksichtigen Sie dabei insbesondere einen Näherungswert für f'(0), die Nullstelle von f'und das Verhalten von f'für x→5.
+
Skizzieren Sie in der Abbildung den Graphen der zugehörigen Ableitungsfunktion f'. Berücksichtigen Sie dabei insbesondere einen Näherungswert für f'(0), die Nullstelle von f' und das Verhalten von f' für x→5.
  
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
  
−
[[Bild:ABI2017_AI_TeilA_4ab_Lös.jpg|700px]]
+
[[Bild:ABI2012_AI_TeilA_4_Lös.jpg|700px]]
 
}}
 
}}
  

Aktuelle Version vom 17. April 2018, 16:38 Uhr


Mathematik (Bayern): Abiturprüfung 2012
Analysis I - Teil A


Download der Originalaufgaben - Lösung zum Ausdrucken


Aufgabe 1

Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an.
a) f(x) = ln(x+3)
b) g(x) = \frac{2}{x^{2}-1}

700px



Aufgabe 2

Geben Sie jeweils den Term einer in IR definierten Funktion an, die die angegebene Eigenschaft besitzt.
a) Der Graph der Funktion f hat den Hochpunkt (0|5) .
b) Die Funktion g ist an der Stelle x = 5 nicht differenzierbar.

700px


Aufgabe 3

Gegeben ist die in IR definierte Funktion f:x \mapsto sin(2x).
a) Geben Sie zwei benachbarte Nullstellen von f an.
b) Berechnen Sie den Wert des bestimmten Integrals \int_{0}^{2} f (x)\,dx .

Warum stimmt der Wert diese Integrals ich mit dem Inhalt der Fläche überein, die für 0 ≤ x ≤ 2 zwischen dem Graphen von f und der x-Achse liegt?
700px


Aufgabe 4
Abitur 2012 Teil A Aufgabengruppe I A4.png

Abbildung 1 zeigt den Graphen Gf einer in ]-∞;5] definierten Funktion f. Skizzieren Sie in der Abbildung den Graphen der zugehörigen Ableitungsfunktion f'. Berücksichtigen Sie dabei insbesondere einen Näherungswert für f'(0), die Nullstelle von f' und das Verhalten von f' für x→5.

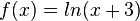
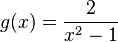
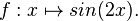
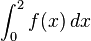700px


Von „http://rmg.zum.de/index.php?title=Abitur_Mathematik/Abi_2012_Analysis_I_Teil_A&oldid=72479“