Abi 2016 Geometrie I Teil B: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | a) | + | In einem kartesischen Koordinatensystem legen die Punkte A(6/3/3) , B(3/6/3) und C(3/3/6) das gleichseitige Dreieck ABC fest.<br /> |
| + | <br /> | ||
| + | |||
| + | a) Ermitteln Sie eine Gleichung der Ebene E, in der das Dreieck ABC liegt, in Normalenform.<br /> | ||
| + | :(mögliches Ergebnis: E: x<sub>1</sub>+x<sub>2</sub>+x<sub>3</sub>-12=0) | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_GI_TeilB_1a_Lös.jpg|700px]] | [[Bild:ABI2016_GI_TeilB_1a_Lös.jpg|700px]] | ||
}} | }} | ||
| − | b) | + | Spiegelt man die Punkte A, B und C am Symmetriezentrum Z(3|3|3), so erhält man die Punkte A', B' bzw. C'.<br /> |
| + | <br /> | ||
| + | b)Beschreiben Sie die Lage der Ebene, in der die Punkte A, B und Z liegen, im Koordinatensystem. Zeigen Sie, dass die Strecke [CC'] senkrecht auf dieser Ebene steht. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_GI_TeilB_1b_Lös.jpg|700px]] | [[Bild:ABI2016_GI_TeilB_1b_Lös.jpg|700px]] | ||
}} | }} | ||
| − | c) | + | c)Begründen Sie, dass das Viereck ABA'B' ein Quadrat mit der Seitenlänge 3√2 ist. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_GI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2016_GI_TeilB_1c_Lös.jpg|700px]] | ||
}} | }} | ||
| − | + | [[Bild:ABI2016_GI_TeilB_1d.png|right|250px]]<br /> | |
| − | [[Bild:ABI2016_GI_TeilB_1d. | + | |
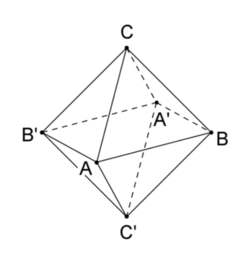
| + | Der Körper ABA'B'CC' ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat ABA'B' als gemeinsamer Grundfläche und den Pyramidenspitzen C bzw. C'. | ||
| + | |||
| + | d) Weisen Sie nach, dass das Oktaeder das Volumen 36 besitzt. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 45: | Zeile 54: | ||
}} | }} | ||
| − | e) | + | e) Bestimmen Sie die Größe des Winkels zwischen den Seitenflächen ABC und |
| + | AC'B. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_GI_TeilB_1e_Lös.jpg|700px]] | [[Bild:ABI2016_GI_TeilB_1e_Lös.jpg|700px]] | ||
}} | }} | ||
| − | f) | + | f)Alle Eckpunkte des Oktaeders liegen auf einer Kugel. Geben Sie eine Gleichung dieser Kugel an. |
| + | Berechnen Sie den Anteil des Oktaedervolumens am Kugelvolumen. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_GI_TeilB_1f_Lös.jpg|700px]] | [[Bild:ABI2016_GI_TeilB_1f_Lös.jpg|700px]] | ||
| Zeile 56: | Zeile 67: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
</div> | </div> | ||
Aktuelle Version vom 28. März 2018, 15:00 Uhr
|
|
In einem kartesischen Koordinatensystem legen die Punkte A(6/3/3) , B(3/6/3) und C(3/3/6) das gleichseitige Dreieck ABC fest. a) Ermitteln Sie eine Gleichung der Ebene E, in der das Dreieck ABC liegt, in Normalenform.
Spiegelt man die Punkte A, B und C am Symmetriezentrum Z(3|3|3), so erhält man die Punkte A', B' bzw. C'. c)Begründen Sie, dass das Viereck ABA'B' ein Quadrat mit der Seitenlänge 3√2 ist. Der Körper ABA'B'CC' ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat ABA'B' als gemeinsamer Grundfläche und den Pyramidenspitzen C bzw. C'. d) Weisen Sie nach, dass das Oktaeder das Volumen 36 besitzt. e) Bestimmen Sie die Größe des Winkels zwischen den Seitenflächen ABC und AC'B. f)Alle Eckpunkte des Oktaeders liegen auf einer Kugel. Geben Sie eine Gleichung dieser Kugel an. Berechnen Sie den Anteil des Oktaedervolumens am Kugelvolumen. |