Abi 2017 Analysis II Teil B: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 23: | Zeile 23: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | Gegeben ist die Funktion f mit f(x)= 2e<sup>-x</sup> | + | Gegeben ist die Funktion f mit '''f(x)= 2e<sup>-x</sup>⋅(2e<sup>-x</sup> - 1)''' und x ∈ IR. <br /> |
| − | und x ∈ IR. | + | Abbildung 1 zeigt den Graphen G<sub>f</sub> von f sowie die einzige Nullstelle x=ln2 von f. |
| − | Abbildung 1 zeigt den Graphen G<sub>f</sub> | + | |
| − | von f sowie die einzige | + | |
| − | + | ||
| − | + | ||
| − | x | + | |
| − | + | ||
| − | von f | + | |
| − | . | + | |
| + | [[Bild:ABI2017_AII_TeilB_1.jpg|center|350px]] | ||
| − | + | a)Zeigen Sie, dass für den Term der Ableitungsfunktion f' von f gilt: '''f'(x)=2e<sup>-x</sup>⋅(1-4e<sup>-x</sup>)''' | |
| − | a) | + | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 42: | Zeile 34: | ||
}} | }} | ||
| − | b) | + | b) Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von G<sub>f</sub> .<br /> |
| + | : (Teilergebnis: x-Koordinate des Extrempunkts: ln4) | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2017_AII_TeilB_1b_Lös.jpg|700px]] | [[Bild:ABI2017_AII_TeilB_1b_Lös.jpg|700px]] | ||
}} | }} | ||
| + | <br /> | ||
| + | Zusätzlich ist die Funktion F mit '''F(x)=2e<sup>-x</sup>-2e<sup>-2x</sup>''' und x∈IR gegeben.<br /> | ||
| − | c) | + | c) Zeigen Sie, dass F eine Stammfunktion von f ist, und begründen Sie anhand des Terms von F, dass <math> \lim_{x\to+\infty}F(x)=0 </math> gilt. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 28. März 2018, 13:13 Uhr
|
|
Gegeben ist die Funktion f mit f(x)= 2e-x⋅(2e-x - 1) und x ∈ IR. a)Zeigen Sie, dass für den Term der Ableitungsfunktion f' von f gilt: f'(x)=2e-x⋅(1-4e-x) b) Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von Gf .
c) Zeigen Sie, dass F eine Stammfunktion von f ist, und begründen Sie anhand des Terms von F, dass d) e) f) g) h) |
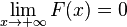 gilt.
gilt.

