Abi 2016 Analysis II Teil A: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“) |
|||
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
| − | <center>[https://www.isb.bayern.de/download/ | + | <center>[https://www.isb.bayern.de/download/17845/abiturpruefung_mathematik_2016_pruefungsteil_a.pdf'''Download der Originalaufgaben'''] - [[Media:Abiturprüfung Mathematik 2017/Teil A|Lösung zum Ausdrucken]] </center> |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | 1 Gegeben ist die Funktion | + | 1) Gegeben ist die Funktion <math>f(x)= \frac{ln(x)}{x^2}</math> mit maximalem Definitionsbereich D. <br> <br> |
| − | f | + | a) Geben Sie D sowie die Nullstelle von f an und bestimmen Sie <math>\lim_{x\to 0}</math> f(x). <br> <br> |
| − | x | + | b) Ermitteln Sie die x-Koordinate des Punkts, in dem der Graph von f eine |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
waagrechte Tangente hat. | waagrechte Tangente hat. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2016_AII_TeilA_1ab_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 49: | Zeile 44: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | 2) Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt. <br> <br> | ||
| + | a) Der Punkt ( 2 | 0 ) ist ein Wendepunkt des Graphen von g. <br> <br> | ||
| + | b) Der Graph der Funktion h ist streng monoton fallend und rechtsgekrümmt. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2016_AII_TeilA_2ab_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 67: | Zeile 65: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| + | 3) Abbildung 1 zeigt den Graphen der in IR definierten Funktion f. | ||
| + | [[Bild:ABI2016_AII_TeilA_3.jpg|center|350px]] | ||
| + | |||
| + | a) Bestimmen Sie mithilfe von Abbildung 1 einen Näherungswert für <math> \int_{3}^{5} f (x)\,dx </math>. <br> <br> | ||
| + | Die Funktion F ist die in IR definierte Stammfunktion von f mit F(3) = 0. <br> <br> | ||
| + | b) Geben Sie mithilfe von Abbildung 1 einen Näherungswert für die Ableitung von F an der Stelle x = 2 an. <br> <br> | ||
| + | c) Zeigen Sie, dass <math> F(b) = \int_{3}^{b} f (x)\,dx </math> mit b ∈ IR gilt. | ||
| + | |||
| + | |||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2016_AII_TeilA_3abc_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 84: | Zeile 92: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
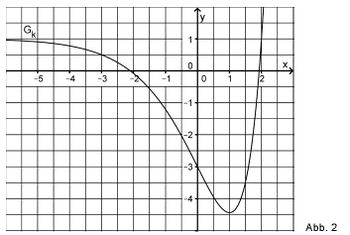
| + | 4) Abbildung 2 zeigt den Graphen G<sub>k</sub> einer in IR definierten Funktion k. Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion k'. Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen G<sub>k</sub> an dessen Wendepunkt ( 0 | -3 ) sowie die Nullstelle von k'. | ||
| + | [[Bild:ABI2016_AII_TeilA_4.jpg|center|350px]] | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2016_AII_TeilA_4_Lös.jpg|700px]] |
}} | }} | ||
Aktuelle Version vom 26. Juli 2017, 08:18 Uhr
|
|
1) Gegeben ist die Funktion
|
2) Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.
|
3) Abbildung 1 zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe von Abbildung 1 einen Näherungswert für
|
4) Abbildung 2 zeigt den Graphen Gk einer in IR definierten Funktion k. Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion k'. Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen Gk an dessen Wendepunkt ( 0 | -3 ) sowie die Nullstelle von k'. |
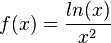 mit maximalem Definitionsbereich D.
mit maximalem Definitionsbereich D. 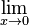 f(x).
f(x). 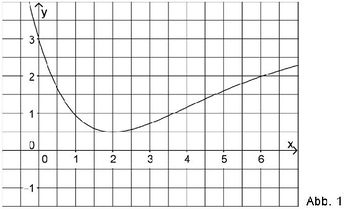
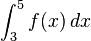 .
. 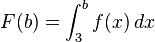 mit b ∈ IR gilt.
mit b ∈ IR gilt.