Abi 2012 Analysis II Teil A: Unterschied zwischen den Versionen
| Zeile 26: | Zeile 26: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_1_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 47: | Zeile 47: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_2ab_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 66: | Zeile 66: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_3ab_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 85: | Zeile 85: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_4ab_Lös.jpg|700px]] |
}} | }} | ||
Aktuelle Version vom 25. Juli 2017, 05:38 Uhr
|
|
Gegeben ist die Funktion
|
Gegeben ist die in IR definierte Funktion |
Betrachtet wird die in IR+ definierte Funktion |
a) Warum hat jede Integralfunktion mindestens eine Nullstelle? |
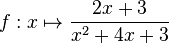 mit maximaler Definitionsmenge D. Bestimmen Sie D sowie die Nullstelle von f.
mit maximaler Definitionsmenge D. Bestimmen Sie D sowie die Nullstelle von f.
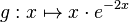
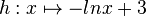 .
. 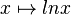 hervorgeht.
hervorgeht. 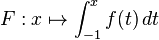 genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von F an.
genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von F an.

