Abi 2012 Analysis II Teil A: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | + | Gegeben ist die Funktion <math> f:x \mapsto \frac{2x+3}{x^{2}+4x+3}</math> mit maximaler Definitionsmenge D. Bestimmen Sie D sowie die Nullstelle von f. | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_1_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 41: | Zeile 41: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | + | Gegeben ist die in IR definierte Funktion <math> g:x\mapsto x \cdot e^{-2x} </math> <br> | |
| + | a) Bestimmen Sie die Koordinaten des Punkts, in dem der Graph von g eine waagrechte Tangente hat. <br> | ||
| + | b) Geben Sie das Verhalten von g für x→-∞ und x→∞ an. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_2ab_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 59: | Zeile 61: | ||
;Aufgabe 3 | ;Aufgabe 3 | ||
| − | + | Betrachtet wird die in IR<sup>+</sup> definierte Funktion <math> h:x \mapsto -lnx+3 </math>. <br> | |
| + | a) Geben Sie an, wie der Graph von h schrittweise aus dem Graphen der in IR<sup>+</sup> definierten Funktion <math> x \mapsto lnx </math> hervorgeht. <br> | ||
| + | b) Bestimmen Sie die Gleichung der Tangente an den Graphen von h im Punkt (1/h(1)) | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_3ab_Lös.jpg|700px]] |
}} | }} | ||
| Zeile 76: | Zeile 80: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
| − | + | a) Warum hat jede Integralfunktion mindestens eine Nullstelle? <br> | |
| − | + | b) Geben Sie den Term einer in IR definierten Funktion f an, sodass die in IR definierte Integralfunktion <math> F:x \mapsto \int_{-1}^{x} f (t)\,dt </math> genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von F an. | |
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI2012_AII_TeilA_4ab_Lös.jpg|700px]] |
}} | }} | ||
Aktuelle Version vom 25. Juli 2017, 05:38 Uhr
|
|
Gegeben ist die Funktion
|
Gegeben ist die in IR definierte Funktion |
Betrachtet wird die in IR+ definierte Funktion |
a) Warum hat jede Integralfunktion mindestens eine Nullstelle? |
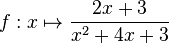 mit maximaler Definitionsmenge D. Bestimmen Sie D sowie die Nullstelle von f.
mit maximaler Definitionsmenge D. Bestimmen Sie D sowie die Nullstelle von f.
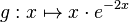
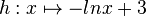 .
. 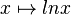 hervorgeht.
hervorgeht. 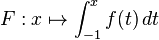 genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von F an.
genau zwei Nullstellen besitzt. Geben Sie die Nullstellen von F an.

