Abi 2015 Analysis I Teil B: Unterschied zwischen den Versionen
| Zeile 11: | Zeile 11: | ||
| − | <center>[https://www.isb.bayern.de/download/ | + | <center>[https://www.isb.bayern.de/download/16162/abiturpruefung_mathematik_2015_pruefungsteil_b.pdf '''Download der Originalaufgaben'''] - [[Media:Abiturprüfung Mathematik 2017/Teil B|Lösung zum Ausdrucken]] </center> |
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 23. Juli 2017, 18:04 Uhr
|
|
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
b) Begründen Sie, dass die x-Achse horizontale Asymptote von Gf ist, und geben Sie die Gleichungen der vertikalen Asymptoten von Gf an. Be-
stimmen Sie die Koordinaten des Schnittpunkts von Gf mit der y-Achse. Abbildung 1 zeigt den Graphen der in IR definierten Funktion c)Gemäß der Quotientenregel gilt für die Ableitungen f und p die Beziehung : Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von fx und px, dass x2 einzige Nullstelle von f ist und dass fG in 3; 2 streng monoton steigend sowie in 2; 1 streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von f G an.
d)Berechnen Sie f(5) und f(1,5) und skizzieren sie Gf unter Berücksichtigung der Ergebnisse in Abbildung 1.
|
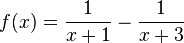 und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
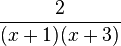 ;
;
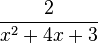 ;
;
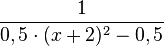

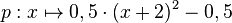 , die die Nullstellen
, die die Nullstellen 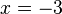 und
und 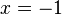 hat.
Für
hat.
Für 



