Abi 2012 Analysis I Teil A: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 43: Zeile 43:
  
 
;Aufgabe 2
 
;Aufgabe 2
−
 
+
Geben Sie jeweils den Term einer in IR definierten Funktion an, die die angegebene Eigenschaft besitzt. <br>
 +
a) Der Graph der Funktion f hat den Hochpunkt (0|5) .<br>
 +
b) Die Funktion g ist an der Stelle x = 5 nicht differenzierbar.
  
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=
Zeile 62: Zeile 64:
 
;Aufgabe 3
 
;Aufgabe 3
  
 +
Gegeben ist die in IR definierte Funktion <math> f:x \mapsto sin(2x). </math> <br>
 +
a) Geben Sie zwei benachbarte Nullstellen von f an. <br>
 +
b) Berechnen Sie den Wert des bestimmten Integrals <math> \int_{0}^{2} f (x)\,dx </math>. <br>
 +
: Warum stimmt der Wert diese Integrals ich mit dem Inhalt der Fläche überein, die für 0 ≤ x ≤ 2 zwischen dem Graphen von f und der x-Achse liegt?
  
 
:{{Lösung versteckt|1=
 
:{{Lösung versteckt|1=

Version vom 20. Juli 2017, 17:33 Uhr


Mathematik (Bayern): Abiturprüfung 2012
Analysis I - Teil A


Download der Originalaufgaben - Lösung zum Ausdrucken


Aufgabe 1

Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an.
a) f(x) = ln(x+3)
b) g(x) = \frac{2}{x^{2}-1}

700px



Aufgabe 2

Geben Sie jeweils den Term einer in IR definierten Funktion an, die die angegebene Eigenschaft besitzt.
a) Der Graph der Funktion f hat den Hochpunkt (0|5) .
b) Die Funktion g ist an der Stelle x = 5 nicht differenzierbar.

700px


Aufgabe 3

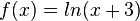
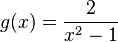
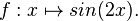
Gegeben ist die in IR definierte Funktion f:x \mapsto sin(2x).
a) Geben Sie zwei benachbarte Nullstellen von f an.
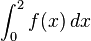b) Berechnen Sie den Wert des bestimmten Integrals \int_{0}^{2} f (x)\,dx .

Warum stimmt der Wert diese Integrals ich mit dem Inhalt der Fläche überein, die für 0 ≤ x ≤ 2 zwischen dem Graphen von f und der x-Achse liegt?
700px


Aufgabe 4


700px


Von „http://rmg.zum.de/index.php?title=Abitur_Mathematik/Abi_2012_Analysis_I_Teil_A&oldid=69632“