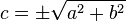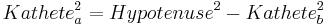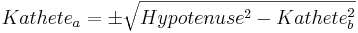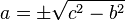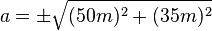Ergänzungen: Unterschied zwischen den Versionen
K (Andrea Schellmann verschob Seite Hier erarbeitest du Ergänzungen dazu nach 9d 2014 15/Satz des Pythagoras/Ergänzungen: eindeutige Zuordnung zu übergeordneter Seite) |
|||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[9d 2014 15/Mathematik/Satz des Pythagoras|Satz des Pythagoras]] | ||
| + | |||
Da wir ausschließlich den Flächeninhalt eines Quadrats bestimmt haben, können wir die Seitenlänge dieses Quadrats bestimmen, indem wir die Wurzel ziehen: | Da wir ausschließlich den Flächeninhalt eines Quadrats bestimmt haben, können wir die Seitenlänge dieses Quadrats bestimmen, indem wir die Wurzel ziehen: | ||
<br /><math>Hyoptenuse=\pm\sqrt{Kathete_a^2+Kathete_b^2}</math><br /> | <br /><math>Hyoptenuse=\pm\sqrt{Kathete_a^2+Kathete_b^2}</math><br /> | ||
| − | Ergänze | + | :<br /><math>c=\pm\sqrt{a^2+b^2}</math><br /> |
| + | |||
| + | |||
| + | Ergänze beides in deinem Heft! | ||
| + | |||
Da wir Streckenlängen betrachten, ist es nicht nötig, die negative Lösung mit anzugeben. Mathematisch korrekt sind beide Lösungen! | Da wir Streckenlängen betrachten, ist es nicht nötig, die negative Lösung mit anzugeben. Mathematisch korrekt sind beide Lösungen! | ||
Wenn wir die Seitenlänge einer Kathete bestimmen wollen, müssen wir die Formel zunächst umstellen! | Wenn wir die Seitenlänge einer Kathete bestimmen wollen, müssen wir die Formel zunächst umstellen! | ||
| + | |||
| + | |||
'''Arbeitsauftrag:''' | '''Arbeitsauftrag:''' | ||
Forme den Satz des Pythagoras so um, dass du die Seitenlänge einer Kathete bestimmen kannst! | Forme den Satz des Pythagoras so um, dass du die Seitenlänge einer Kathete bestimmen kannst! | ||
| + | |||
<popup name="Seitenlänge der Kathete"> erste Umformung ergibt: <br /><math>{Kathete_a^2=Hypotenuse^2-Kathete_b^2\,}</math> | <popup name="Seitenlänge der Kathete"> erste Umformung ergibt: <br /><math>{Kathete_a^2=Hypotenuse^2-Kathete_b^2\,}</math> | ||
| − | zweite Umformung ergibt: <math>Kathete_a=\pm\sqrt{Hypotenuse^2-Kathete_b^2}</math><br /></popup> | + | zweite Umformung ergibt: <math>Kathete_a=\pm\sqrt{Hypotenuse^2-Kathete_b^2}</math><br /> |
| + | <br /><math>a=\pm\sqrt{c^2-b^2}</math><br /> | ||
| + | </popup> | ||
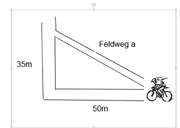
Bestimme nun die Streckenlänge, die der Fahrradfahrer bei Feldweg a zurücklegen muss! | Bestimme nun die Streckenlänge, die der Fahrradfahrer bei Feldweg a zurücklegen muss! | ||
| + | Du kannst rechts auch nochmal das Bild vergrößern! | ||
| + | |||
| + | [[Datei:Fahrradfahrer neu.png|thumb|Problem des Fahrradfahrers]] | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | ungefähr 61,03m | + | <br /><math>a=\pm\sqrt{(50m)^2+(35m)^2}</math><br /> also ungefähr 61,03m |
</popup> | </popup> | ||
| Zeile 26: | Zeile 40: | ||
ja, es ist eine Abkürzung, da er auf der Straße 35m + 50m = 85m zurücklegen muss! | ja, es ist eine Abkürzung, da er auf der Straße 35m + 50m = 85m zurücklegen muss! | ||
</popup> | </popup> | ||
| + | |||
| + | Hier geht's wieder zurück: | ||
| + | [[9d 2014 15/Mathematik/Satz des Pythagoras|Satz des Pythagoras]] | ||
Aktuelle Version vom 20. November 2014, 18:16 Uhr
Da wir ausschließlich den Flächeninhalt eines Quadrats bestimmt haben, können wir die Seitenlänge dieses Quadrats bestimmen, indem wir die Wurzel ziehen:
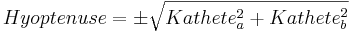
Ergänze beides in deinem Heft!
Da wir Streckenlängen betrachten, ist es nicht nötig, die negative Lösung mit anzugeben. Mathematisch korrekt sind beide Lösungen!
Wenn wir die Seitenlänge einer Kathete bestimmen wollen, müssen wir die Formel zunächst umstellen!
Arbeitsauftrag:
Forme den Satz des Pythagoras so um, dass du die Seitenlänge einer Kathete bestimmen kannst!
Bestimme nun die Streckenlänge, die der Fahrradfahrer bei Feldweg a zurücklegen muss! Du kannst rechts auch nochmal das Bild vergrößern!
Ist dies nun eine Abkürzung? Entscheide rechnerisch deine Antwort!
Hier geht's wieder zurück: Satz des Pythagoras