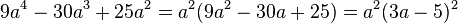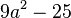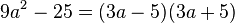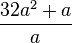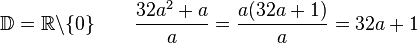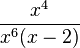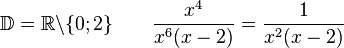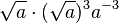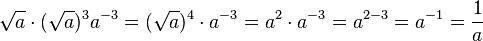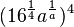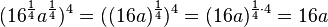Term und Zahl: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (typo) |
|||
| (17 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <br /> | ||
| + | __NOTOC__ | ||
| + | <div style="background: #ABAABF"> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <center><table border=0 width="800px" cellpadding=5 cellspacing=5> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | |||
| + | {| | ||
| + | |width="70%"| | ||
| + | |||
== Teste dein Wissen== | == Teste dein Wissen== | ||
| − | |||
<br /> | <br /> | ||
| − | + | '''1. Vereinfache folgende Terme soweit wie möglich.'''<br /> | |
| − | + | <math>\frac48 a-( \frac24 a- \frac93 b) =</math> | |
| − | + | <popup name="Lösung"> | |
| − | <math>\frac48 a-( \frac24 a- \frac93 b) =</math> | + | <math>=\frac48 a- \frac24 a+ \frac93 b=3b </math> |
| − | <math> - | + | </popup> <br/> |
| − | </ | + | |
| + | <math> -x(-1+x)-(3+x)(4-x)+13=</math> | ||
| + | <popup name="Lösung"> | ||
| + | <math> =x-x^2-(12-3x+4x-x^2)+13=x-x^2-12-x+x^2+13=1</math> | ||
| + | </popup> <br /> | ||
| − | 2.Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht. <br /> | + | '''2. Setze im ersten Term die Klammern so, dass eine richtige Termumformung entsteht. <br />''' |
<math>-2a^2+4a \cdot 2 - a = 8a</math> | <math>-2a^2+4a \cdot 2 - a = 8a</math> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
| Zeile 21: | Zeile 37: | ||
</popup> <br /> | </popup> <br /> | ||
| − | + | '''3. Klammere den größtmöglichen Faktor aus.<br/> ''' | |
| − | 3.Klammere den größtmöglichen Faktor aus.<br/> | + | |
<math> 12xy^2-18xy+15x^2y</math> | <math> 12xy^2-18xy+15x^2y</math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| Zeile 32: | Zeile 47: | ||
</math></popup><br/> | </math></popup><br/> | ||
| + | |width="10%"| | ||
| − | 4.Faktorisiere den Term (mit Hilfe der binomischen Formeln)<br/> | + | |valign="top"| |
| + | |||
| + | == Knicktests == | ||
| + | <br/> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | [[Datei:1 AB1 Terme.pdf|thumb|Knicktest Termumformungen, Faktorisieren|200px|zentriert]] | ||
| + | |||
| + | |} | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | |||
| + | {| | ||
| + | |width="70%"| | ||
| + | |||
| + | '''4. Faktorisiere den Term (mit Hilfe der binomischen Formeln).<br/>''' | ||
<math> 9a^2-30a+25</math> | <math> 9a^2-30a+25</math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| − | <math> 9a^2-30a+25=(3a-5)^2 | + | <math> 9a^2-30a+25=(3a-5)^2 </math> <br/> 2.binomische Formel</popup><br/> |
| − | </math></popup><br/> | + | |
<math>9a^4-30a^3+25a^2 </math> | <math>9a^4-30a^3+25a^2 </math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| − | <math> 9a^4-30a^3+25a^2=a^2(9a^2-30a+25)=a^2(3a-5)^2 a | + | <math> 9a^4-30a^3+25a^2=(3a^2-5a)^2 </math> 2. binomische Formel <br/> |
| − | + | <math> 9a^4-30a^3+25a^2=a^2(9a^2-30a+25)=a^2(3a-5)^2 </math> <br/> a<sup>2</sup> ausklammern +2.binomische Formel | |
| + | </popup><br/> | ||
<math>9a^2-25 </math> | <math>9a^2-25 </math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| − | <math> 9a^2-25=(3a-5)(3a+5) 3.binomische Formel | + | <math> 9a^2-25=(3a-5)(3a+5)</math><br/> 3.binomische Formel |
| − | </ | + | </popup><br/> |
| − | + | |width="10%"| | |
| + | |[[Datei:1 AB2 BinFormeln.pdf|thumb|Knicktest Binomische Formeln|200px|zentriert]] | ||
| + | |} | ||
| + | <br /> | ||
| + | <br /> | ||
| − | 5. Gib die Definitionsmenge an und vereinfache soweit wie möglich<br/> | + | {| |
| + | |width="70%"| | ||
| + | '''5. Gib die Definitionsmenge an und vereinfache soweit wie möglich.<br/>''' | ||
<math> \frac{32a^2+a}{a}</math> | <math> \frac{32a^2+a}{a}</math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| Zeile 56: | Zeile 95: | ||
<math> \frac{x^4}{x^6(x-2)}</math> | <math> \frac{x^4}{x^6(x-2)}</math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| − | <math>\mathbb{D} =\mathbb{R} \backslash \{0 | + | <math>\mathbb{D} =\mathbb{R} \backslash \{0;2\} \qquad \frac{x^4}{x^6(x-2)}= \frac{1}{x^2(x-2)} |
</math></popup><br/> | </math></popup><br/> | ||
| + | |width="10%"| | ||
| + | |[[Datei:1 AB4 Bruchterme.pdf|thumb|Knicktest Bruchterme|200px|zentriert]] | ||
| + | |} | ||
| + | <br /> | ||
| + | <br /> | ||
| − | + | {| | |
| − | 6 | + | |width="70%"| |
| + | '''6. Vereinfache soweit wie möglich (a>0) <br/>''' | ||
<math> \sqrt a \cdot (\sqrt a)^3 a^{-3} </math> | <math> \sqrt a \cdot (\sqrt a)^3 a^{-3} </math> | ||
<popup name = "Lösung"> | <popup name = "Lösung"> | ||
| − | <math> \sqrt a \cdot (\sqrt a)^3 a^{-3} = (\sqrt a)^4 \cdot a^{-3} = a^2 \cdot a^{-3}=a^{2-3}=a^{-1} \frac1 a | + | <math> \sqrt a \cdot (\sqrt a)^3 a^{-3} = (\sqrt a)^4 \cdot a^{-3} = a^2 \cdot a^{-3}=a^{2-3}=a^{-1} =\frac1 a |
</math></popup><br/> | </math></popup><br/> | ||
<math> (16^{\frac1 4} a^{\frac1 a})^4</math> | <math> (16^{\frac1 4} a^{\frac1 a})^4</math> | ||
| Zeile 73: | Zeile 118: | ||
<math> 8^x:2^x=(8:2)^x=4^x | <math> 8^x:2^x=(8:2)^x=4^x | ||
</math></popup><br/> | </math></popup><br/> | ||
| + | |width="10%"| | ||
| + | |[[Datei:1_AB3_Potenzen.pdf|thumb|Knicktest Potenzen und Wurzeln|200px|zentriert]] | ||
| + | |} | ||
| + | |||
| + | [[Mathematik_Grundwissen_10|Zurück zur Übersicht]] | ||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 25. September 2014, 17:57 Uhr
|
|
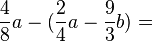
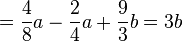
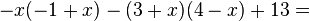
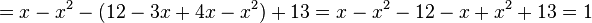
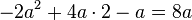
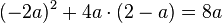
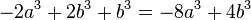
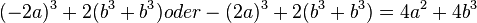
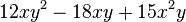
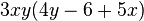
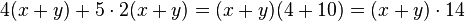

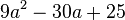
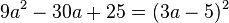
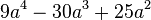
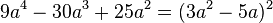 2. binomische Formel
2. binomische Formel