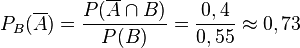Stochastik: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
{| | {| | ||
| − | |width=" | + | |width="70%"| |
== Teste dein Wissen== | == Teste dein Wissen== | ||
| Zeile 27: | Zeile 27: | ||
</popup> <br /> | </popup> <br /> | ||
| + | |width="5%"| | ||
| + | |valign="top"| | ||
| + | == Knicktests == | ||
| + | [[Datei:4 AB1.pdf|thumb|Knicktest - Laplace-Experimente & Mehrstufige Zufallsexperimente (Pfadregeln)]] | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |width="70%"| | ||
'''2) Nebenstehende Vierfeldertafel gehört zu einem zweistufigen Zufallsexperiment mit den zwei Ereignissen A und B. <br/> | '''2) Nebenstehende Vierfeldertafel gehört zu einem zweistufigen Zufallsexperiment mit den zwei Ereignissen A und B. <br/> | ||
| Zeile 73: | Zeile 81: | ||
<math> P_B (\overline{A}) = \frac {P(\overline{A} \cap B)} {P(B)} = \frac {0,4} {0,55} \approx 0,73 </math> | <math> P_B (\overline{A}) = \frac {P(\overline{A} \cap B)} {P(B)} = \frac {0,4} {0,55} \approx 0,73 </math> | ||
</popup> | </popup> | ||
| + | |||
| + | |width="5%"| | ||
| + | |valign="top"| | ||
| + | <br/> | ||
| + | <br/> | ||
| + | [[Datei:4 AB2.pdf|thumb|Knicktest - Mehrstufige Zufallsexperimente (Baumdiagramm, Vierfeldertafel, Bedingte Wahrscheinlichkeit)]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | [[Mathematik_Grundwissen_10|Zurück zur Übersicht]] | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | </div> | ||
Version vom 11. September 2014, 12:54 Uhr
|
|

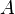
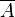
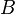
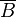
 B ein
B ein
 B ein
B ein