Diagramme: Unterschied zwischen den Versionen
K |
|||
| (32 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | <div style="margin: | + | '''2. Stunde''' <br /> |
| + | <div style="margin:0px; margin-right:0px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> | ||
| + | {{Lernpfad Mechanik}} | ||
| + | '''<span style="color: blue"><big>Zeichnen von Diagrammen</big></span>''' | ||
| + | {|width="100%" | ||
| + | |width="40%" style="vertical-align:top"| | ||
| − | |||
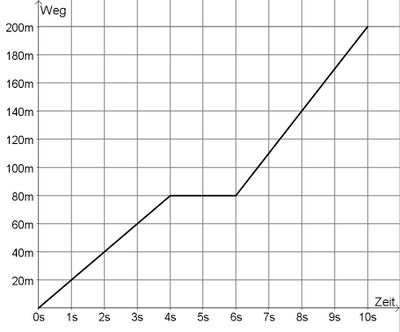
| − | + | Es wurde die zurückgelegte Strecke und die dafür benötigte Zeit bei einem Pkw gemessen. Hier ist das Ergebnis dargestellt: | |
| + | {| border="1" cellspacing="0" valign="top" | ||
| + | | width="14%" | Zeit in s | ||
| + | | width="8%" | 0 | ||
| + | | width="8%" | 1,0 | ||
| + | | width="8%" | 2,0 | ||
| + | | width="8%" | 3,0 | ||
| + | | width="8%" | 4,0 | ||
| + | | width="8%" | 5,0 | ||
| + | | width="8%" | 6,0 | ||
| + | | width="8%" | 7,0 | ||
| + | | width="8%" | 8,0 | ||
| + | | width="8%" | 9,0 | ||
| + | | width="8%" | 10,0 | ||
| + | |-valign="top" | ||
| + | | Weg in m | ||
| + | | 0 | ||
| + | | 20 | ||
| + | | 40 | ||
| + | | 60 | ||
| + | | 80 | ||
| + | | 80 | ||
| + | | 80 | ||
| + | | 110 | ||
| + | | 140 | ||
| + | | 170 | ||
| + | | 200 | ||
| + | |} | ||
<br /> | <br /> | ||
| + | <big>'''Aufgabe 2:'''</big> <br /> | ||
| + | '''a) Was sollte man alles beim Zeichnen eines Diagrammes beachten?''' | ||
| − | + | <div class="zuordnungs-quiz"> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | {| | ||
| + | | Wichtig! || Achsenbeschriftung mit den Größen und Einheiten vornehmen || Diagramm so zeichnen, dass alle Messwerte in die Zeichnung passen || Diagramm groß genug zeichnen, sodass es nachher deutlich erkennbar ist | ||
| + | |- | ||
| + | | Nicht so wichtig oder falsch || Die passende Farbe für das Diagramm auswählen || Die Messwerte mit einem dicken Punkt einzeichnen, sodass sie jeder von Weitem erkennen kann || Auch wenn die Werte auf der Achse bis 100 gehen, müssen die Zahlen von 1-100 am Rand stehen | ||
|} | |} | ||
| + | |||
</div> | </div> | ||
| + | <br /> | ||
| − | |||
| − | + | '''b) Zeichne das passende s-t-Diagramm (Strecke bzw. Weg - Zeit) zur oben aufgeführten Wertetabelle in dein Heft. Kontrolliere dein Vorgehen im Anschluss noch einmal dabei mit Teilaufgabe a)!''' | |
| − | + | <br /> | |
| + | <popup name="Hinweis"> | ||
| + | - die waagerechte Achse ist die Zeitachse (t-Achse) | ||
| + | </popup> <br /> | ||
| + | <popup name="Lösung"> | ||
| + | [[Datei:Zeit Weg Diagramm Aufgabe2.jpg|thumb|Zeit Weg Diagramm Aufgabe2|center|400px]] | ||
| + | </popup> | ||
| + | |||
| + | |||
| + | '''c) Versuche die Bewegung des Pkws in mehrere Zeitabschnitte sinnvoll zusammenzufassen und gib diese an!''' | ||
| + | <br /> | ||
| + | <popup name="Lösung"> | ||
| + | Es ist sinnvoll diejenigen Abschnitte zusammenzufassen, in denen die Geschwindigkeit gleich bleibt (die Änderung des Ortes von Schritt zu Schritt bleibt hier gleich!) <br /> | ||
| + | 1. Abschnitt: 0s bis 4s <br /> | ||
| + | 2. Abschnitt: 4s bis 6s <br /> | ||
| + | 3. Abschnitt: 6s bis 10s <br /> | ||
| + | </popup> <br /> | ||
| + | |||
| + | '''d) Berechne nun die Geschwindigkeit des Pkws in den einzelnen Zeitabschnitten (aus Teilaufgabe c))''' | ||
| + | |||
| + | <popup name="Lösung"> | ||
| + | Die Geschwindigkeit in den einzelnen Intervallen wird mit der Formel <math>v = \frac{\Delta s}{\Delta t}</math> berechnet. Es ergeben sich folgende Werte: <br /> | ||
| + | 1. Abschnitt: 0s bis 4s <math>v = \frac{\Delta s}{\Delta t} = \frac{80m}{4s} = 20 \frac{m}{s} </math> <br /> | ||
| + | <br /> | ||
| + | 2. Abschnitt: 4s bis 6s <math>v = \frac{0m}{2s} = 0 \frac{m}{s} </math> <br /> | ||
| + | <br /> | ||
| + | 3. Abschnitt: 6s bis 10s <math>v = \frac{120m}{4s} = 30 \frac{m}{s} </math> <br /> | ||
| + | </popup> <br /> | ||
| + | <br /> | ||
| + | '''e) Berechne die durchschnittliche Geschwindigkeit des Pkws insgesamt in m/s und km/h! Stelle diese in deinem Diagramm dar!''' | ||
| + | <popup name="Lösung"> | ||
| + | Der Pkw legt insgesamt 200m in 10s zurück. Die Geschwindigkeit ist somit <math>v = \frac{\Delta s}{\Delta t} = \frac{200m}{10s} = 20 \frac{m}{s} </math> . <br /> | ||
| + | Dies sind 72 <math> \frac{km}{h} </math> . <br /> | ||
| + | Die durchschnittliche Geschwindigkeit kann durch eine Strecke vom Startpunkt bis zum Endpunkt dargestellt werden (also von (0|0) bis (10|200)). | ||
| + | </popup> <br /> | ||
| + | <br /> | ||
| + | '''f) Löse das multiple-choice-quiz!''' | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | Zu welchem Zeitpunkt ist die Geschwindigkeit v am größten? | ||
| + | (!3s) (7s) (!5s) (!2s) | ||
| + | |||
| + | Wie schnell müsste der Pkw fahren, damit er die gesamte Strecke s in t = 4s zurücklegt? | ||
| + | (!20m/s) (50m/s) (!10m/s) (!60m/s) | ||
| + | |||
| + | Wie lange braucht der Pkw für die gesamte Strecke, wenn er mit einer durchschnittlichen Geschwindigkeit von v = 20m/s fährt? | ||
| + | (!40s) (!5s) (!20s) (10s) | ||
| + | |||
| + | Was bedeutet ein steil ansteigender Geradenabschnitt? | ||
| + | (!Die Geschwindigkeit ist ziemlich klein) (!Keine Aussage über die Geschwindigkeit möglich) (Die Geschwindigkeit ist ziemlich groß) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | <br /> | ||
| + | <br /> | ||
| + | <big>'''Aufgabe 3:'''</big> <br /> | ||
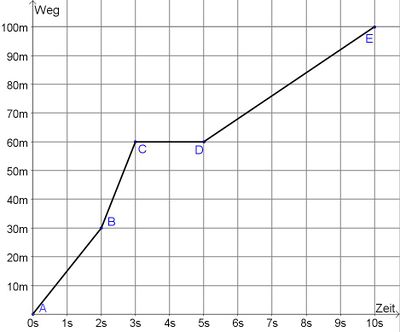
| + | Das s-t-Diagramm stellt die Bewegung eines Pkw´s da. Berechne die Geschwindigkeit zwischen den Zeitpunkten A,B,C,D und E. Gib alle Geschwindigkeiten in m/s und km/h an! Alle benötigten Rechnungen müssen ins Heft geschrieben werden! | ||
| + | <br /> | ||
| + | [[Datei:Zeit Weg Diagramm.jpg|thumb|Zeit Weg Diagramm|center|400px]] | ||
| + | |||
| + | <popup name="Kontrolle der Ergebnisse"> | ||
| + | Geschwindigkeit zwischen den Punkten <br /> | ||
| + | AB: v = 15m/s <br /> | ||
| + | BC: v = 30m/s <br /> | ||
| + | CD: v = 0m/s <br /> | ||
| + | DE: v = 8m/s <br /> | ||
| + | </popup> <br /> | ||
| + | <br /> | ||
Aktuelle Version vom 4. März 2014, 21:39 Uhr
2. Stunde
|
Zeichnen von Diagrammen
|
d) Berechne nun die Geschwindigkeit des Pkws in den einzelnen Zeitabschnitten (aus Teilaufgabe c))
Zu welchem Zeitpunkt ist die Geschwindigkeit v am größten? (!3s) (7s) (!5s) (!2s) Wie schnell müsste der Pkw fahren, damit er die gesamte Strecke s in t = 4s zurücklegt? (!20m/s) (50m/s) (!10m/s) (!60m/s) Wie lange braucht der Pkw für die gesamte Strecke, wenn er mit einer durchschnittlichen Geschwindigkeit von v = 20m/s fährt? (!40s) (!5s) (!20s) (10s) Was bedeutet ein steil ansteigender Geradenabschnitt? (!Die Geschwindigkeit ist ziemlich klein) (!Keine Aussage über die Geschwindigkeit möglich) (Die Geschwindigkeit ist ziemlich groß)
|
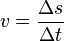 berechnet. Es ergeben sich folgende Werte:
berechnet. Es ergeben sich folgende Werte: 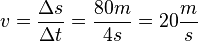
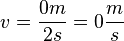
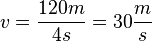
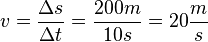 .
. 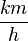 .
.