Geschwindigkeit: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 46: | Zeile 46: | ||
</div> | </div> | ||
| − | Die Formel zur Berechnung lautet: Geschwindigkeit <math> = {zurückgelegte Strecke /over dafür benötigte Zeit} </math> oder <math> v = { | + | Die Formel zur Berechnung lautet: Geschwindigkeit <math> = {zurückgelegte Strecke /over dafür benötigte Zeit} </math> oder <math> v = {/Delta s /over /Delta t} </math> (Gesprochen: <math> /Delta </math> delta) <br /> |
| − | " | + | "<math> /Delta </math> s" bedeutet die Strecke am Ende - die Strecke am Anfang. (Das ist wichtig, wenn wir zum Beispiel die Geschwindigkeit in den letzten 6 Metern der Bewegung des Pkws ausrechnen wollen.) |
Version vom 2. November 2013, 17:11 Uhr
= Lernpfad zur Einführung in die Mechanik =
1. Stunde
Geschwindigkeit und Beschleunigung
Ein großes Teilgebiet der Mechanik ist die Kinematik (den Wortteil "Kin" kennst du aus dem Kino: dort werden Bilder bewegt. Kinematik bedeutet also Bewegung.).
Fangen wir direkt mit der einfachsten Art der Fortbewegung an:
Der geradlinig gleichförmigen Bewegung.
a) Berechne mit Hilfe des Videos die durchschnittliche Geschwindigkeit des Pkws insgesamt.
b) Berechne nun die durchschnittliche Geschwindigkeit des Pkws auf den ersten 6 Metern.
c) Wie kannst du die Geschwindigkeit auf den letzten 6 Metern ausrechnen? Versuche eine allgemeine Formel anzugeben.
Bearbeite folgenden Lückentext:
Möchte man die durchschnittliche Geschwindigkeit eines Körpers berechnen, so dividiert man die zurückgelegte Strecke durch die dafür benötigte Zeit.
Teilt man dabei eine Strecke in der Einheit Meter durch die Zeit in der Einheit Sekunde so erhält man folglich die Geschwindigkeit in der Einheit 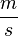
Die Formel zur Berechnung lautet: Geschwindigkeit Fehler beim Parsen(Lexikalischer Fehler): = {zurückgelegte Strecke /over dafür benötigte Zeit}
oder(Gesprochen:
delta)
"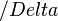 s" bedeutet die Strecke am Ende - die Strecke am Anfang. (Das ist wichtig, wenn wir zum Beispiel die Geschwindigkeit in den letzten 6 Metern der Bewegung des Pkws ausrechnen wollen.)
s" bedeutet die Strecke am Ende - die Strecke am Anfang. (Das ist wichtig, wenn wir zum Beispiel die Geschwindigkeit in den letzten 6 Metern der Bewegung des Pkws ausrechnen wollen.)

