Integralberechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
===Berechnung des Wasservolumens in den ersten sechs Monaten=== | ===Berechnung des Wasservolumens in den ersten sechs Monaten=== | ||
| − | '''''<span style="color: darkorange">Ermittle für a = 3 | + | '''''<span style="color: darkorange">Ermittle für a = 3 wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.</span> |
{| | {| | ||
|width=400px| | |width=400px| | ||
| − | :''Um Auszurechnen, | + | :''Um Auszurechnen, wie viel Kubikliter Wasser durch den Fluss fließen, errechnet man die Fläche unter der Funktion''. |
| Zeile 15: | Zeile 15: | ||
{|width=90%| style="background-color:#F5F5F5; border: 1px solid #63B8FF; padding:0.5em" | {|width=90%| style="background-color:#F5F5F5; border: 1px solid #63B8FF; padding:0.5em" | ||
| valign="top" | | | valign="top" | | ||
| − | :Die allgemeine Integrationsregel: <math>\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}</math> | + | :Die allgemeine Integrationsregel: <math>\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}</math> <ref>''Barth, Friedrich / Mühlbauer, Paul / Nikol, Friedrich / Wörle Karl,'' Mathematische Formeln und Definitionen, München <math>2004^8</math>, S.66</ref> |
|} | |} | ||
:<small>a ist die untere Grenze, b die obere. Die Funktion wird im Intervall [ a; b ] integriert.</small> | :<small>a ist die untere Grenze, b die obere. Die Funktion wird im Intervall [ a; b ] integriert.</small> | ||
| − | ::<u>'''<span style="color: red">Merke:</span>'''</u> | + | ::<u>'''<span style="color: red">Merke:</span>'''</u> |
| + | ::Das bestimmte Integral einer Funktion <math>f (x)</math> im Intervall[] <math>\left [ a , b \right ]</math> ist aber nicht immer definiert, sondern nur dann, wenn die Funktion im Intervall <math>\left [ a , b \right ]</math>stetig ist. Die Funktion darf also keine Sprünge haben.<ref>[http://www.mathematik.net/Integ-1/ia2s9.htm Integrierbarkeit einer Funktion]</ref> | ||
|width=5px| | |width=5px| | ||
|valign="top" | | |valign="top" | | ||
| − | <ggb_applet width="369" height="458" version="3.2" ggbBase64=" | + | <ggb_applet width="369" height="458" version="3.2" ggbBase64="UEsDBBQACAAIACB6OzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVZLj9NIED4vv6LlEyyaxI88pWTQLlxGDMshwIEDUtsux820u61+zDj8+q1+OMkMr0GgHNyuqq7HV1+Vs3kxdJzcgtJMim2STdKEgKhkzcR+m1jTXKySF5dPNnuQeygVJY1UHTXbpJjkiZNbdvnkr41u5R2h3Jt8YHC3TRrKNSRE9wporVsAc09O7cA4o+rwtvwMldEnRXByJXqLUYyyKKu6+prp8XXqAjZSGEI0+wKYdO5km6nPZQO24qxmVLh4Pjc0IuSO1abFtBfrhLTA9i26m80XwVslpap3B22gI8NHUBJ168kqO/8l5BA16WyyWi2K2bJYp+t1scAqK8oxkXw1Qcnply3xUtRlq0mxTPP5cjkr1vN1OluF0HC7A2MQbU3oAHosea9YfX6+0v9KXh9R6iUT5iXtjVW+UUUU7czBBcMmKlfiP2LPIcpyxLGF6qaUwy7AVgTX7w69v+LTKfcvJZeKKLwwn6NBfJbh6W1cnker1Nuk3iL6cE6P+mydewv/LMPTW3EmQmqx7mwsOkvHMEwTJ0Dnjl8jHJyWwLfJGymoSYgVzFwHSUIMq25iuVm49J/tSiT3eNcZvEIqUVFBYPv9UNm3QzHOcTxAkNe2ZDcdGFB/JPJm+oCtmxtQAnjgpEBaWGk1uaV87LxPt4aKdfgaFBFP6nr9HnMK0hr2CqJ9nKmAttem57x/IN5MxyRcDhrTrwxWjxUYV56bXdNK5U41NU7ipo5DBziSxpNJ2A4Uq44A0sRFwxA2BipG5P3ikH4HPAD9NOuo/g7dcFv0LcXTJIukogdQ90r03t7IOgaOdhpBR8OOjTuvowNOtjvRUktuDewqxE9cy4oavxpDcnGNZGnqbPHOYukOB7zsDw0b4DSmCBP7gn2k9+o5Md+0yAoBWvvxNOeDSAW22OOOW6mPWeoenHd/Hq1Jj0X7JXBkCNIqtMM1ZsANrN12H4FtcMMP6LF5OjwjW4LOyJRg6eRvMnx6ip15Ri4IDW+5e3tOaDyhLCHTr9rdWOEpkpxCPLrOP0WA9JEESB/dg3MUK9l1VNRE0A7VV8LgdFHuq2TuS0VoGgDFjLKQDqE5evSw0liGNaNpGQJEtz+dn/Lh/OTL3xugLM2/QnD+QwTfNo0G4xh/kWeR8D+asF8EeHq+avzHPP7huPwfUEsHCD4VaMlsAwAAoggAAFBLAQIUABQACAAIACB6Ozw+FWjJbAMAAKIIAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAApgMAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
|} | |} | ||
| Zeile 29: | Zeile 30: | ||
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| − | ::<math>\ | + | ::<math>\int f (t)\,dt = \frac{1}{16}t^4 - \frac{a \cdot t^3}{3} + \frac{a^2 \cdot t^2}{2} + c = F (t)</math> |
::Die obere Grenze ist: 6 <small> ''Nach den ersten sechs Monaten''</smalL> | ::Die obere Grenze ist: 6 <small> ''Nach den ersten sechs Monaten''</smalL> | ||
| Zeile 35: | Zeile 36: | ||
::Die untere Grenze ist: 0 | ::Die untere Grenze ist: 0 | ||
| − | ::<math>\int_{0}^{6} f (t)\,dt = </math> <math>\left[ \frac{1}{16}t^4 - \frac{3 | + | ::<math>\int_{0}^{6} f (t)\,dt = </math> <math>\left[ \frac{1}{16}t^4 - \frac{3 \cdot t^3}{3} + \frac{3^2 \cdot t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27</math> |
| − | ::<u>Für a = 3 fließen in den ersten sechs Monaten 27 | + | ::<u>Für a = 3 fließen in den ersten sechs Monaten 27 <math>\cdot </math> 10<sup>9</sup> Liter Wasser durch den Fluss.</u> (<small> 27 <math>\cdot</math> 10<sup>6</sup> m<sup>3</sup> = 27 <math>\cdot</math> 10<sup>9</sup> Liter</small>) |
}} | }} | ||
| − | [ | + | ::Falls du mit der Integration noch Schwierigkeiten haben solltest, gibt es [http://de.sevenload.com/sendungen/Nachhilfe-2-0/folgen/s8j162f-Flaeche-berechnen-Grenzen-gegeben-Integralrechnung hier] einen nützlichen Link. |
| − | [[ | + | |
| + | [[LK Mathematik Abitur NRW 2007/Flächengleichheit|Hier geht's zur Aufgabe: Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t<sub>0</sub>]], | ||
| + | |||
| + | [[LK Mathematik Abitur NRW 2007|Hier geht's zurück zur Übersicht]] | ||
| + | |||
| + | ==Quellen== | ||
| + | <references/> | ||
Aktuelle Version vom 6. Februar 2011, 15:55 Uhr
Berechnung des Wasservolumens in den ersten sechs Monaten
Ermittle für a = 3 wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
|
|
- Gebe die Funktion F (t) an und errechne mit ihr für a = 3, wieviel Liter in den ersten sechs Monaten durch den Fluss geflossen sind.
- Die obere Grenze ist: 6 Nach den ersten sechs Monaten
- Die untere Grenze ist: 0
- Für a = 3 fließen in den ersten sechs Monaten 27
 109 Liter Wasser durch den Fluss. ( 27
109 Liter Wasser durch den Fluss. ( 27  106 m3 = 27
106 m3 = 27  109 Liter)
109 Liter)
- Für a = 3 fließen in den ersten sechs Monaten 27
- Falls du mit der Integration noch Schwierigkeiten haben solltest, gibt es hier einen nützlichen Link.
Hier geht's zur Aufgabe: Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t0,
Hier geht's zurück zur Übersicht
Quellen
- ↑ Barth, Friedrich / Mühlbauer, Paul / Nikol, Friedrich / Wörle Karl, Mathematische Formeln und Definitionen, München
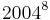 , S.66
, S.66
- ↑ Integrierbarkeit einer Funktion
![\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}](/images/math/c/4/e/c4e09d0a32630fc2d68d22072dd7ccd8.png)
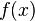 im Intervall[]
im Intervall[] ![\left [ a , b \right ]](/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png) ist aber nicht immer definiert, sondern nur dann, wenn die Funktion im Intervall
ist aber nicht immer definiert, sondern nur dann, wenn die Funktion im Intervall 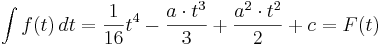
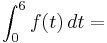
![\left[ \frac{1}{16}t^4 - \frac{3 \cdot t^3}{3} + \frac{3^2 \cdot t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27](/images/math/f/7/1/f71e9edb8b764bb660fd0ac14ab9482b.png)

