Übungen: Unterschied zwischen den Versionen
Aus RMG-Wiki
< Lernpfad Flächenberechnung/Inhaltsverzeichnis | Parallelogramm | Flächenberechnung | Hefteintrag
| Zeile 20: | Zeile 20: | ||
:'''Alle vier Seiten sind gleich lang.'''}} | :'''Alle vier Seiten sind gleich lang.'''}} | ||
| − | Verschiebe die Raute so, dass du eine Figur mit vier rechten Winkeln erhälst. {{versteckt| | + | Verschiebe die Raute an den Punkten A und C so, dass du eine Figur mit vier rechten Winkeln erhälst. {{versteckt| |
:'''Es entsteht ein Quadrat.'''}} | :'''Es entsteht ein Quadrat.'''}} | ||
| Zeile 28: | Zeile 28: | ||
Eigenschaften: {{versteckt| | Eigenschaften: {{versteckt| | ||
:'''Alle vier Seiten sind gleich lang.''' | :'''Alle vier Seiten sind gleich lang.''' | ||
| − | + | }} | |
Aktuelle Version vom 1. November 2010, 19:16 Uhr
|
|
Hier siehst du eine Sonderform des Parallelogramms.
Was fällt dir auf?
- Alle vier Seiten sind gleich lang.
Verschiebe die Raute an den Punkten A und C so, dass du eine Figur mit vier rechten Winkeln erhälst.
- Es entsteht ein Quadrat.
Ich erkenne:
- Die Raute ist ein verschobenes Quadrat.
Eigenschaften:
- Alle vier Seiten sind gleich lang.
Überlege und Begründe
Eine Raute hat wie ein Quadrat vier gleich lange Seiten. Hat sie auch den selben Flächeninhalt wie ein Quadrat?
Hilfe:
- Verschiebe den Punkt A und C und beobachte. Was passiert mit dem Flächeninhalt?
Lösung:
- Der Flächeninhalt der Raute ist kleiner als der Flächeninhalt des Quadrats, weil die Höhe abnimmmt.
Arbeitsauftrag:
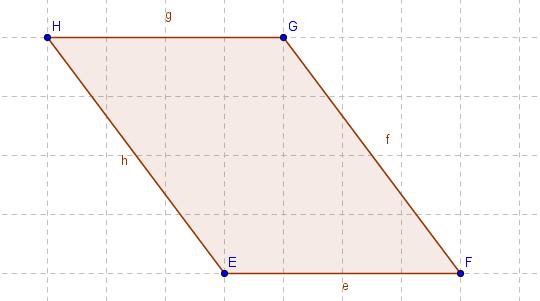
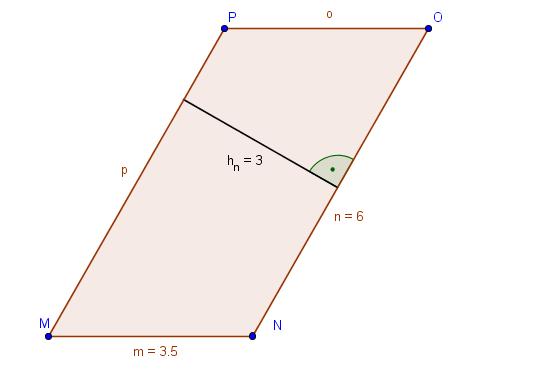
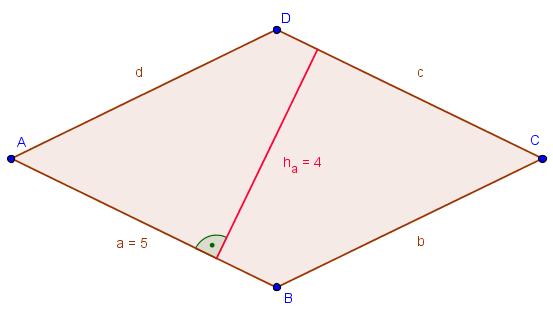
- Berechne die Flächeninhalte der Parallelogramme.
- Kontrolliere deine Ergebnisse mit den Ergebnissen auf der Seite.
- 1 Kästchen = 1 cm
- Anmerkung: AParallelogramm = Grundlinie
 HöheGrundlinie
HöheGrundlinie
|
Übung 1:
A |
|
Übung 2:
A |
|
Übung 3:
A |
Hier geht's weiter!

 a
a