Geometrie: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(link zurück eingefügt)
(-rest)
 
(39 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
zurück zu [[Jahr der Mathematik]]
+
__NOTOC__
 +
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
 +
[[Jahr der Mathematik/Gedichte|'''Gedichte''']] '''·''' [[Jahr der Mathematik/Geschichten|'''Geschichten''']]  '''·''' [[Jahr der Mathematik/besondere Zahlen|'''Besondere Zahlen''']] '''·''' [[Jahr der Mathematik/Zahlen im Alltag|'''Zahlen im Alltag''']] '''·''' [[Jahr der Mathematik/Potenzen|'''Potenzen''']] '''·''' [[Jahr der Mathematik/Rap|'''Mathe-Rap''']] '''·''' [[Jahr der Mathematik/Kalender|'''Kalender''']] '''·'''  [[Jahr der Mathematik/Geometrie|'''Geometrie''']] '''·''' [[Jahr der Mathematik/Symmetrie|'''Symmetrie''']] '''·'''  [[Jahr der Mathematik/Übungen|'''Memory, Quiz und Co. ''']]
 +
</div>
 +
==Geometrische Bilder==
  
 +
;Kreisbilder mit GeoGebra
 +
[[Bild:Esther Kreis 1a 200px.jpg]]
 +
[[Bild:Adrian Kreis 200px.jpg]]
 +
[[Bild:Kreis_Thomas2_200px.jpg]]
 +
[[Bild:Kreisbild1paulm 200px.jpg]]
  
−
==Schrägbilder==
+
mehr [[Kandinsky-Impressionen mit GeoGebra|Kreisbilder]]
  
 +
==Schrägbilder==
 
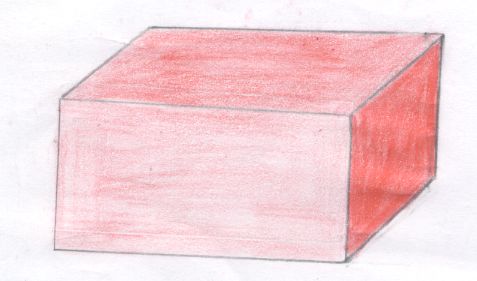
von [[Benutzer:Dominique Gründler|Dominique Gründler]][[Bild:Gründler_schräg.jpg|right]]
 
von [[Benutzer:Dominique Gründler|Dominique Gründler]][[Bild:Gründler_schräg.jpg|right]]
  
−
===Isometrische Schrägbilder von Gebäuden===
+
;Isometrische Schrägbilder von Gebäuden
−
Isometrie ist eigentlich fast das gleiche wie Geometrie, aber eben doch ein bisschen anders, da dreidimensional dargestellt. Am Anfang habe ich nur ein paar Quadrate und Rechtecke gezeichnet, aber dann kam ich auf die Idee, verschiedene Formen in 3D zu zeichnen, wie ihr auf dem Bild rechts sehen könnt.
+
:Isometrie ist eigentlich fast das gleiche wie Geometrie, aber eben doch ein bisschen anders, da dreidimensional dargestellt wird. Am Anfang habe ich nur ein paar Quadrate und Rechtecke gezeichnet, aber dann kam ich auf die Idee, verschiedene Formen in 3D zu zeichnen, wie ihr auf dem Bild rechts sehen könnt.
 +
:Wenn ihr wissen wollt wie Schrägbilder funktionieren, dann lest euch den unteren Text durch.
  
−
Wenn ihr wissen wollt wie Geometrie funktioniert, dann klickt auf diesen Link.
+
;Erklärung zu Schrägbildern
 +
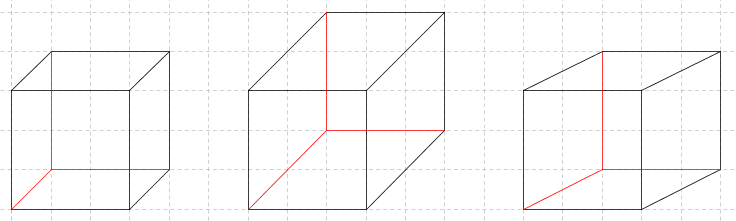
:Um sich einen Körper besser vorstellen zu können, zeichnet man von ihm ein '''Schrägbild'''. Kanten, die in Wirklichkeit parallel sind, sind auch im Schrägbild parallel. Kanten, die in Wirklichkeit aufeinander senkrecht stehen, müssen im Schrägbild nicht aufeinander senkrecht stehen.
 +
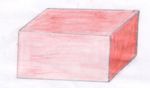
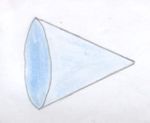
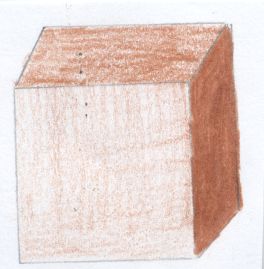
;Die Zeichnungen zeigen verschiedene Schrägbilder eines Würfels.
  
−
[[Übung zu Schrägbildern für Anfänger]]
+
[[Bild:Gründler02.png]]
  
  
−
===Erklärung zu Schrägbildern===
 
  
−
Um sich einen Körper besser vorstellen zu können, zeichnet man von ihm ein '''Schrägbild'''.  
+
[[bild:Gründler03.png|left]]
−
Kanten, die in Wirklichkeit parallel sind, sind auch im Schrägbild parallel. Kanten, die in Wirklichkeit aufeinander senkrecht stehen, müssen im Schrägbild nicht aufeinander senkrecht stehen.
+
Welches der drei Zeichnungen sieht am ehesten nach einem Würfel aus?
  
−
Die Zeichnungen zeigen verschiedene Schrägbilder eines Würfels.
+
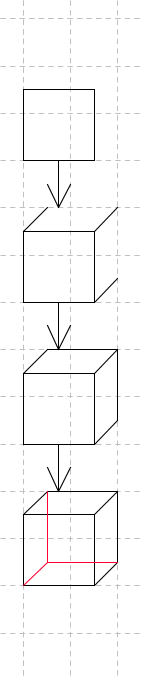
;Übung für Anfänger "Schrägbild eines Würfels"
  
 +
:#Nehmt erstmal ein kariertes Blatt Papier und einen Bleistift zur Hand. Vielleicht noch ein Geodreieck, falls ihr es braucht.
  
  
−
==Geometrische Bilder==
 
  
−
===Kreisbilder mit GeoGebra===
+
:#Zeichnet ein Quadrat.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
:#Zeichnet dann, in einem Winkel von 45°, drei Schrägen an die rechten drei Ecken. Sie dürfen nicht so lang sein wie die Seiten des ersten Quadrates (wegen der perspektivischen Verkürzung!)
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
Wenn ihr das gemacht habt, verbindet sie miteinander.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
 
 +
So, nun seid ihr fast fertig. Aber ihr müsst, um das Schrägbild noch offensichtlicher zu machen, eine gestrichelte Schräge (hier rot eingezeichnet) an der unteren linken Ecke nach innen zeichnen. Zeichnet danach eine gestrichelte (hier ebenfalls rote), senkrechte Linie nach oben, vom Ende der gestrichelten Schräge.
 +
Gut!
 +
Nun kommt eine gestrichelte (hier rote), waagrechte Linie nach rechts, wieder vom Ende der gestrichelten Schräge.
 +
 
 +
 
 +
 
 +
 
 +
'''Geschafft!!!!!'''
 +
 
 +
Nun habt ihr das Schrägbild eines Würfels.
 +
 
 +
 
 +
 
 +
 
 +
 
 +
== Memory zu Körpern ==
 +
 
 +
 
 +
[[Bild:Zylinder100.jpg|150px]]
 +
[[Bild:Prisma2_100.jpg]]
 +
[[Bild:Quader100.jpg|150px]]
 +
[[Bild:Würfel100.jpg|150px]]
 +
[[Bild:Kegel100.jpg|150px]]
 +
[[Bild:Pyramide100.jpg]]
 +
 
 +
 
 +
:Diese Körper heißen '''Zylinder, Prisma, Quader, Würfel, Kegel, Pyramide'''.
 +
 
 +
 
 +
:Hier gibt es ein Memory dazu!
 +
:::{| style="background-color:#F4A460; spacing:0em; padding:0em"
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|1=<span style="font-size:25pt">Quader</span>}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|[[Bild:Kegel100.jpg]]}} </center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|1=<span style="font-size:25pt">Prisma</span>}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|[[Bild:Prisma2 100.jpg]]}}</center>
 +
 
 +
|-
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|[[Bild:Würfel100.jpg]]}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|1=<span style="font-size:25pt">Würfel</span>}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|[[Bild:Zylinder100.jpg]]}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|1=<span style="font-size:25pt">Pyramide</span>}}</center>
 +
|-
 +
 
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|1=<span style="font-size:25pt">Kegel</span>}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|1=<span style="font-size:25pt">Zylinder</span>}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|[[Bild:Pyramide100.jpg]]}}</center>
 +
 
 +
| width="150px" height="150px" style="background-color:#FFFFFF"|
 +
<center>{{versteckt|[[Bild:Quader100.jpg]]}}</center>
 +
 
 +
 
 +
|}
 +
 
 +
==  Haus der Vierecke ==
 +
 
 +
Wir wollen euch ein Haus vorstellen, welches aus Vierecken besteht.
 +
 
 +
Die Nr. 1 im Bild (wird noch eingefügt) ist ein Trapez. Ein Trapez ist ein Viereck, das mindestens 2 parallele Seiten hat. Manchmal hat es auch 4 parallele Seiten, dann ist es ein Parallelogramm. Ein Parallelogramm ist also ein spezielles Trapez.
 +
 
 +
Die Nr. 2 ist ein Rechteck. Bei dem Rechteck handelt es sich um einen geometrischen Körper, bei dem jeweils 2 Seiten gleich lang sind.
 +
 
 +
Bei der Nr. 3 handelt es sich um ein Quadrat. Dies ist ein besonderes Viereck, da hier alle Seiten gleich lang sind.
 +
 
 +
Die Nr. 4 ist eine Raute. Die Raute ist ebenfalls ein besonderes Viereck, denn sie ist gleichzeitig auch noch Parallelogramm und Drachenviereck. Bei einer Raute sind immer 2 gegenüberliegende Seiten parallel und je 2 Winkel, die sich gegenüber liegen, gleich groß. Weiterhin  schneiden sich die Diagonalen im gleichen Winkel.
 +
 
 +
Bei der Nr. 5 handelt es sich um ein Parallelogramm. Das Parallelogramm ist ein Viereck, bei dem gegenüberliegende Seiten gleich lang sind.
  
 +
Bei der Nr. 6 handelt es sich um ein Drachenviereck. Ein Drachenviereck kann ein auf der Spitze stehendes Quadrat sein. Dies ist aber nicht zwingend notwendig. Es hat 2 Paare gleich langer Seiten, wobei mindestens ein Paar gleich lang ist. Die Diagonalen halbieren sich.
  
  
 
==Memory zu Strecken und Geraden==
 
==Memory zu Strecken und Geraden==

Aktuelle Version vom 27. September 2010, 23:37 Uhr

Gedichte · Geschichten · Besondere Zahlen · Zahlen im Alltag · Potenzen · Mathe-Rap · Kalender · Geometrie · Symmetrie · Memory, Quiz und Co.

Geometrische Bilder

Kreisbilder mit GeoGebra

Esther Kreis 1a 200px.jpg Adrian Kreis 200px.jpg Kreis Thomas2 200px.jpg Kreisbild1paulm 200px.jpg

mehr Kreisbilder

Schrägbilder

von Dominique Gründler
Gründler schräg.jpg
Isometrische Schrägbilder von Gebäuden
Isometrie ist eigentlich fast das gleiche wie Geometrie, aber eben doch ein bisschen anders, da dreidimensional dargestellt wird. Am Anfang habe ich nur ein paar Quadrate und Rechtecke gezeichnet, aber dann kam ich auf die Idee, verschiedene Formen in 3D zu zeichnen, wie ihr auf dem Bild rechts sehen könnt.
Wenn ihr wissen wollt wie Schrägbilder funktionieren, dann lest euch den unteren Text durch.
Erklärung zu Schrägbildern
Um sich einen Körper besser vorstellen zu können, zeichnet man von ihm ein Schrägbild. Kanten, die in Wirklichkeit parallel sind, sind auch im Schrägbild parallel. Kanten, die in Wirklichkeit aufeinander senkrecht stehen, müssen im Schrägbild nicht aufeinander senkrecht stehen.
Die Zeichnungen zeigen verschiedene Schrägbilder eines Würfels.

Gründler02.png


Gründler03.png

Welches der drei Zeichnungen sieht am ehesten nach einem Würfel aus?

Übung für Anfänger "Schrägbild eines Würfels"
  1. Nehmt erstmal ein kariertes Blatt Papier und einen Bleistift zur Hand. Vielleicht noch ein Geodreieck, falls ihr es braucht.


  1. Zeichnet ein Quadrat.




  1. Zeichnet dann, in einem Winkel von 45°, drei Schrägen an die rechten drei Ecken. Sie dürfen nicht so lang sein wie die Seiten des ersten Quadrates (wegen der perspektivischen Verkürzung!)





Wenn ihr das gemacht habt, verbindet sie miteinander.





So, nun seid ihr fast fertig. Aber ihr müsst, um das Schrägbild noch offensichtlicher zu machen, eine gestrichelte Schräge (hier rot eingezeichnet) an der unteren linken Ecke nach innen zeichnen. Zeichnet danach eine gestrichelte (hier ebenfalls rote), senkrechte Linie nach oben, vom Ende der gestrichelten Schräge. Gut! Nun kommt eine gestrichelte (hier rote), waagrechte Linie nach rechts, wieder vom Ende der gestrichelten Schräge.



Geschafft!!!!!

Nun habt ihr das Schrägbild eines Würfels.



Memory zu Körpern

Zylinder100.jpg Prisma2 100.jpg Quader100.jpg Würfel100.jpg Kegel100.jpg Pyramide100.jpg


Diese Körper heißen Zylinder, Prisma, Quader, Würfel, Kegel, Pyramide.


Hier gibt es ein Memory dazu!
Quader
Kegel100.jpg
Prisma
Prisma2 100.jpg
Würfel100.jpg
Würfel
Zylinder100.jpg
Pyramide
Kegel
Zylinder
Pyramide100.jpg
Quader100.jpg


Haus der Vierecke

Wir wollen euch ein Haus vorstellen, welches aus Vierecken besteht.

Die Nr. 1 im Bild (wird noch eingefügt) ist ein Trapez. Ein Trapez ist ein Viereck, das mindestens 2 parallele Seiten hat. Manchmal hat es auch 4 parallele Seiten, dann ist es ein Parallelogramm. Ein Parallelogramm ist also ein spezielles Trapez.

Die Nr. 2 ist ein Rechteck. Bei dem Rechteck handelt es sich um einen geometrischen Körper, bei dem jeweils 2 Seiten gleich lang sind.

Bei der Nr. 3 handelt es sich um ein Quadrat. Dies ist ein besonderes Viereck, da hier alle Seiten gleich lang sind.

Die Nr. 4 ist eine Raute. Die Raute ist ebenfalls ein besonderes Viereck, denn sie ist gleichzeitig auch noch Parallelogramm und Drachenviereck. Bei einer Raute sind immer 2 gegenüberliegende Seiten parallel und je 2 Winkel, die sich gegenüber liegen, gleich groß. Weiterhin schneiden sich die Diagonalen im gleichen Winkel.

Bei der Nr. 5 handelt es sich um ein Parallelogramm. Das Parallelogramm ist ein Viereck, bei dem gegenüberliegende Seiten gleich lang sind.

Bei der Nr. 6 handelt es sich um ein Drachenviereck. Ein Drachenviereck kann ein auf der Spitze stehendes Quadrat sein. Dies ist aber nicht zwingend notwendig. Es hat 2 Paare gleich langer Seiten, wobei mindestens ein Paar gleich lang ist. Die Diagonalen halbieren sich.


Memory zu Strecken und Geraden

Von „http://rmg.zum.de/index.php?title=Jahr_der_Mathematik/Geometrie&oldid=35820“