Übungsaufgabe: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <br><br> | ||
| + | |||
{|width="95%" | {|width="95%" | ||
|width="30%" style="vertical-align:top"| | |width="30%" style="vertical-align:top"| | ||
| Zeile 30: | Zeile 32: | ||
'''<span style="color: green">'''Arbeitsauftrag:'''</span>''' | '''<span style="color: green">'''Arbeitsauftrag:'''</span>''' | ||
*Berechne Aufgabe a) in deinem Heft. | *Berechne Aufgabe a) in deinem Heft. | ||
| − | *Überlege dir, | + | *Überlege dir, welches Brett der Tischler auswählen wird und '''begründe''' deine Antwort! |
</div> | </div> | ||
Aktuelle Version vom 26. September 2010, 22:53 Uhr
|
Du erinnerst dich sicher noch an die Tischplatte auf der Einführungsseite des Trapezes. Hier noch einmal zur Erinnerung die Maße mit den Fragestellungen.
Eine Tischlerfirma möchte für dieses Modell eine Tischplatte aussägen. Diese soll genau auf die Unterkonstruktion passen, dass sie nicht an den Seiten übersteht. Maße: a = 100 cm, c = 70 cm, ha= 60 cm. a) Jetzt stellt sich der Tischler die Frage: Wie viel Holz brauche ich für die Platte? b) Dem Tischler stehen drei rechteckige Bretter zur Verfügung. Ihre Maße sind: 1. Brett: 75 cm x 65 cm, 2. Brett: 120 cm x 70 cm, 3. Brett: 65 cm x 110 cm. Welches Brett wird er auswählen? |
Arbeitsauftrag:
- Berechne Aufgabe a) in deinem Heft.
- Überlege dir, welches Brett der Tischler auswählen wird und begründe deine Antwort!
| Lösung a)
A A A A A |
Lösung b)
Brett 1: 75 x 90
Brett 2: 120 x 70
Brett 3: 65 x 110
Der Tischler wird Brett 3 wählen, da er weniger Verschnitt hat. |
Hier kommst du zum Hefteintrag "Der Flächeninhalt des Trapezes".


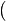 a + c
a + c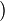
 ha : 2
ha : 2

