Dreieck: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 15: | Zeile 15: | ||
'''Seite 118, Aufgabe 11''' | '''Seite 118, Aufgabe 11''' | ||
| − | {{Lösung versteckt| | + | {{Lösung versteckt| |
| + | Die Diagonale f teilt das Dreieck in zwei gleichgroße Teildreiecke. Die Hälfte der Diagonalen e ist die Höhe der Dreiecke. | ||
| + | |||
| + | '''1. Drachenvierreck:''' | ||
| + | |||
| + | Die Fläche eines Teildreiecks errechnet sich aus: | ||
| + | |||
| + | A<math>=</math> <math>(</math> f<math>\cdot</math>e : 2 <math>)</math> : 2 | ||
| + | |||
| + | A<math>=</math>7 dm <math>\cdot</math> 4 dm : 2 : 2 | ||
| + | |||
| + | A<math>=</math>7 dm² | ||
| + | |||
| + | Das Drachenvierreck besteht aus zwei Teildreiecken. | ||
| + | |||
| + | A<sub>ges</sub><math>=</math>7 dm² + 7 dm² <math>=</math> 14 dm² | ||
| + | |||
| + | <br> | ||
| + | |||
| + | '''2.Drachenvierreck''' | ||
| + | |||
| + | A<math>=</math>80 dm<math>\cdot</math>39 dm : 2<math>\cdot</math>2 | ||
| + | |||
| + | A<math>=</math>3120 dm² | ||
| + | |||
| + | }} | ||
Version vom 21. September 2010, 17:56 Uhr
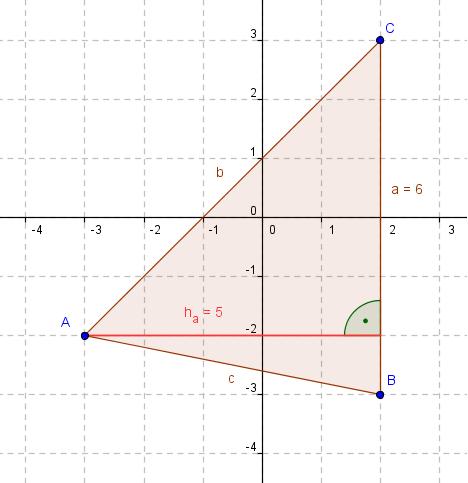
1.Aufgabe
Arbeitsauftrag:
- Zeichne die Punkte A(-3|-2), B(2|-3) unc C(2|3).
- Verbinde sie zu einem Dreieck.
- Berechne die Fläche.
2. Aufgabe
Seite 118, Aufgabe 11
Die Diagonale f teilt das Dreieck in zwei gleichgroße Teildreiecke. Die Hälfte der Diagonalen e ist die Höhe der Dreiecke.
1. Drachenvierreck:
Die Fläche eines Teildreiecks errechnet sich aus:
A
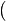 f
f e : 2
e : 2 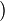 : 2
: 2
A 7 dm
7 dm  4 dm : 2 : 2
4 dm : 2 : 2
A 7 dm²
7 dm²
Das Drachenvierreck besteht aus zwei Teildreiecken.
Ages 7 dm² + 7 dm²
7 dm² + 7 dm²  14 dm²
14 dm²
2.Drachenvierreck
A 80 dm
80 dm 39 dm : 2
39 dm : 2 2
2
A 3120 dm²
3120 dm²
3. Aufgabe
Seite 119, Aufgabe 15 a)
1234